数据结构-图

图

图的定义

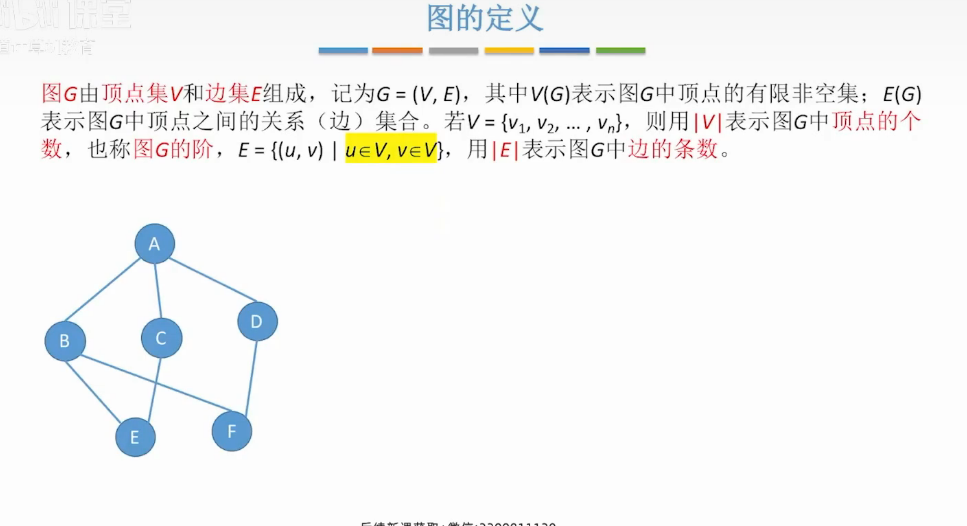
a b c d e f组成顶点集
边集-链接顶点的边组成

图的规则-图的每个边必须有顶点

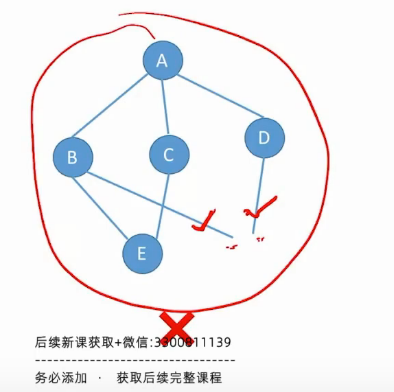
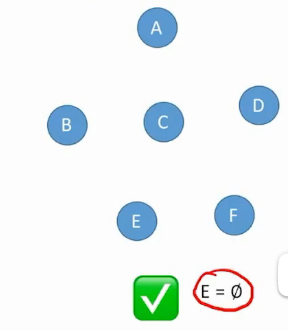
图-的边集可以是空

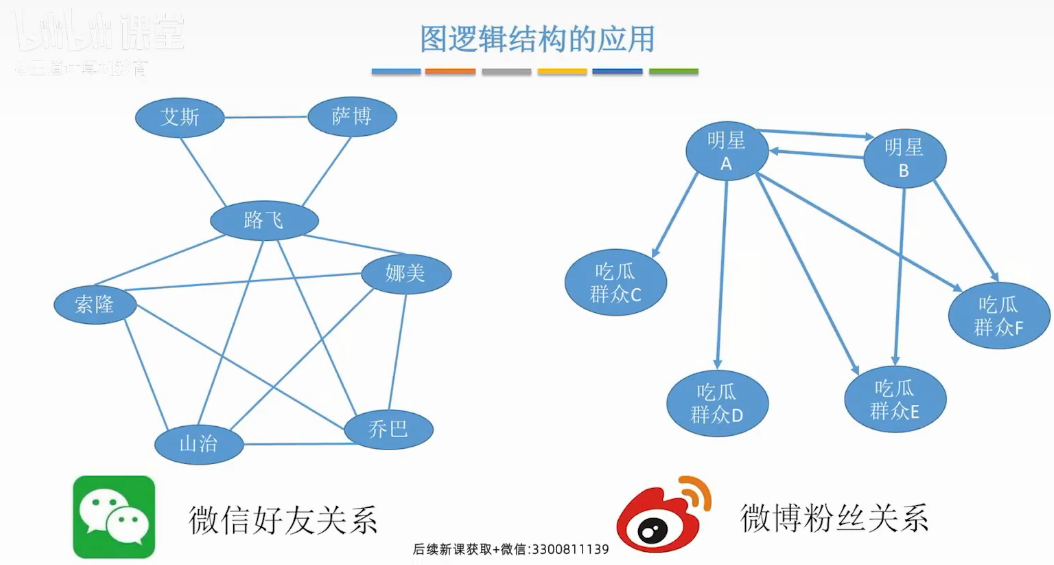
图的逻辑结果应用

图的性质

无向图和有向图

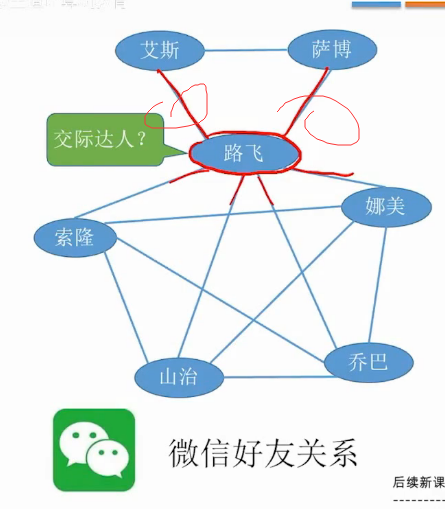
有向图

尾 ->没有箭头
头->有箭头

A->c A弧尾 C弧头

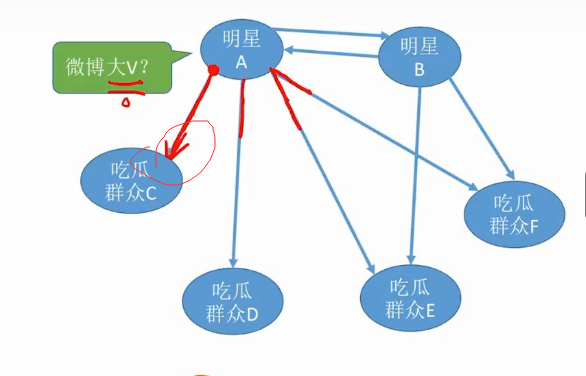
简单图多重图

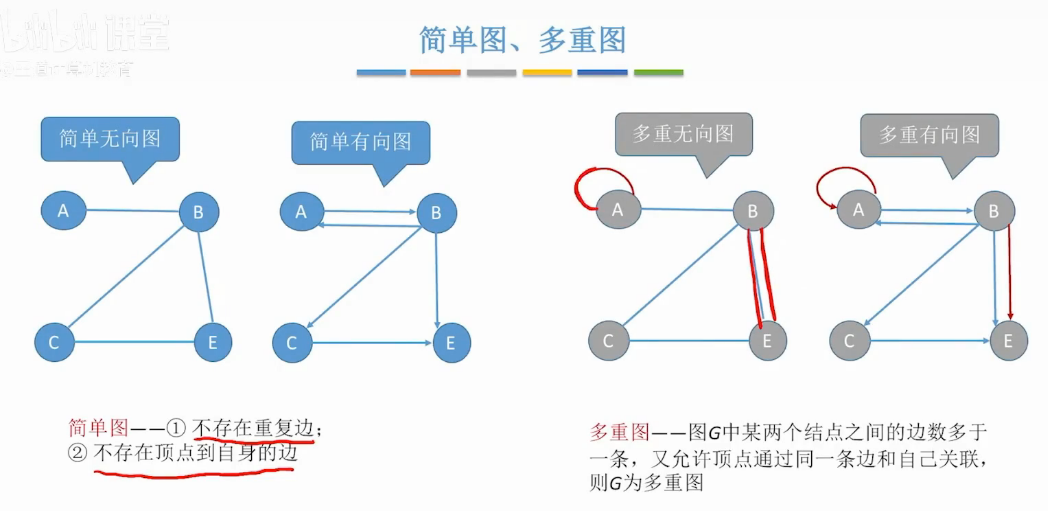
无重边：图中任意两个顶点之间最多只有一条边，即不存在多条边连接同一对顶点。例如 a->b不能再出现一条a->b

无自环：图中不存在连接自身的边，即任何顶点不能有与自身相连的边。

无方向（对于无向图）：边没有方向，即边的连接关系是对称的；有向图则没有此要求。

检查边的数量：查看是否有重复的边。如果有重边，则不是简单图。

检查自环：检查每个顶点是否有连接自身的边。如果有自环，则不是简单图。

确认边的方向（对于无向图）：确保所有边都是无向的，且连接的顶点对是唯一的。

只探讨简单图

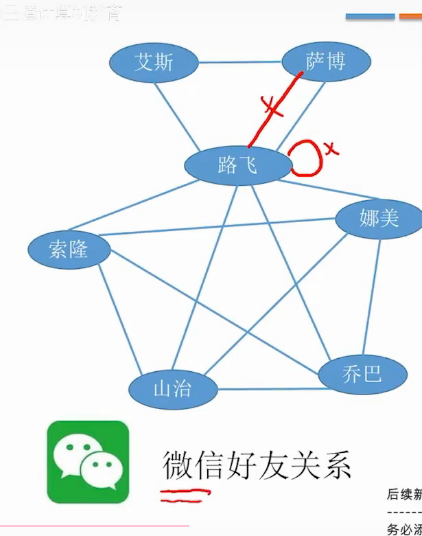
多重 不许自己加自己好友-不许重复加好友

顶点的度 入度 出度

弧尾-hu头

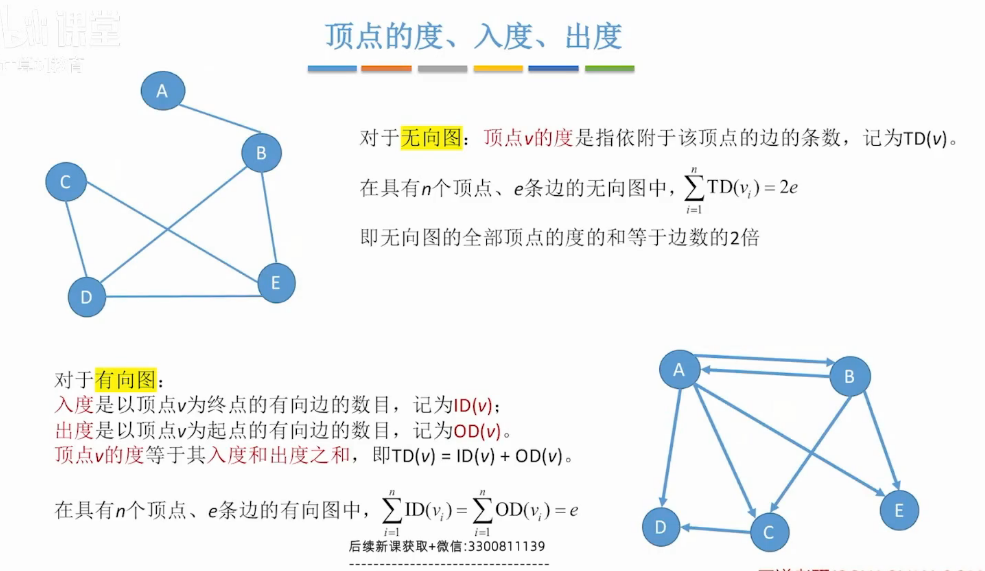
有向图计算 顶点度的计算

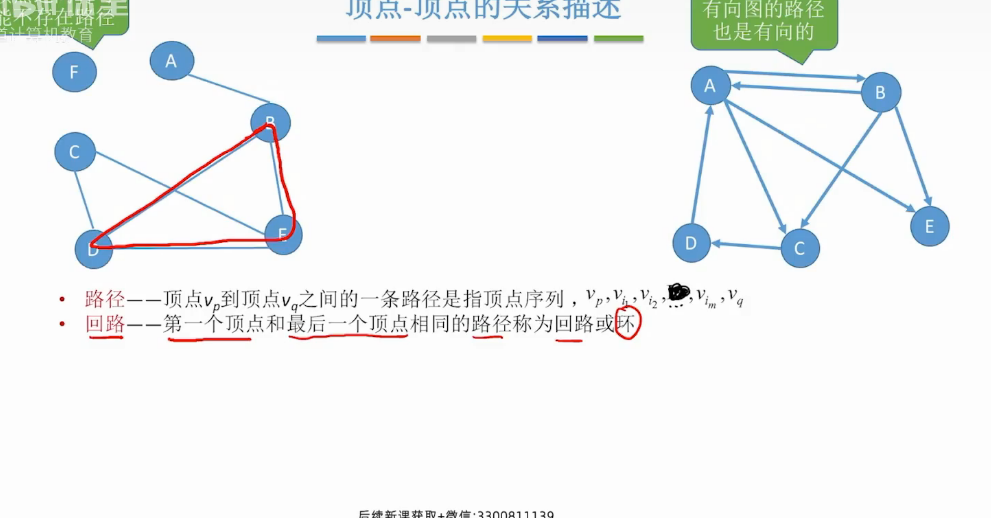
顶点-顶点的关系描述 ***

---

---

---

---

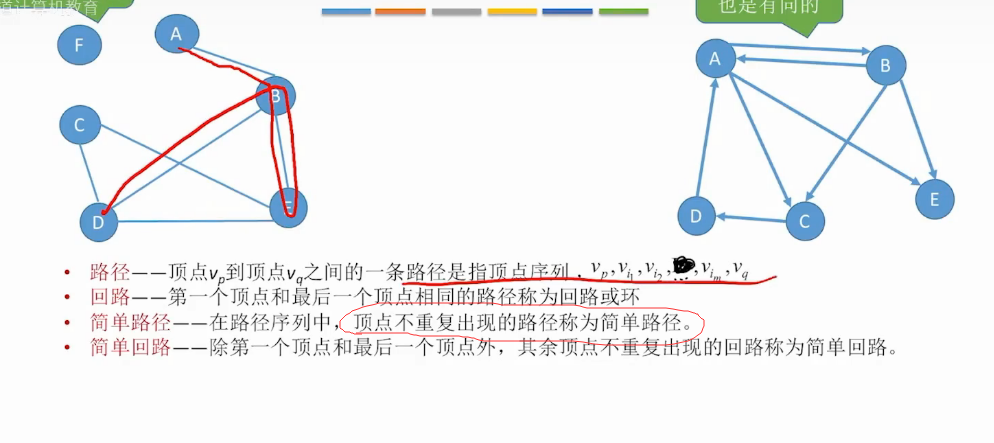
不是简单路径情况-a b a b d ab都重复出现了

---

例如 无向图 F A-无穷 A-B 就是最短路径

---

---

---

---

连通图 强连通图

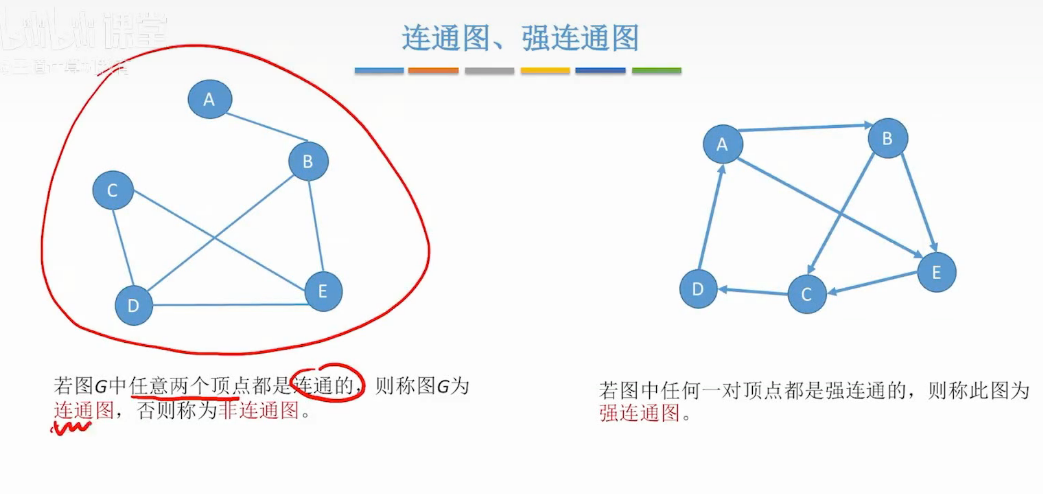
考点**

连通图考点

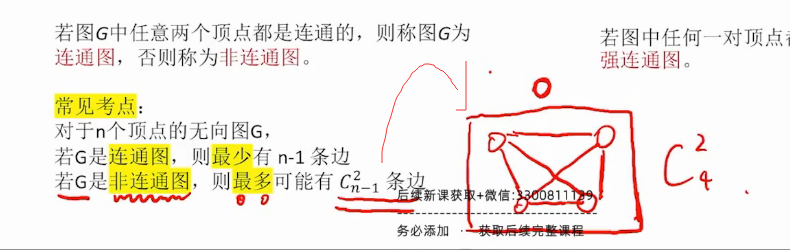
n-1性质

感叹号表示阶乘

5!=5×4×3×2×1=120

4=24

4

6边

图的局部-子图

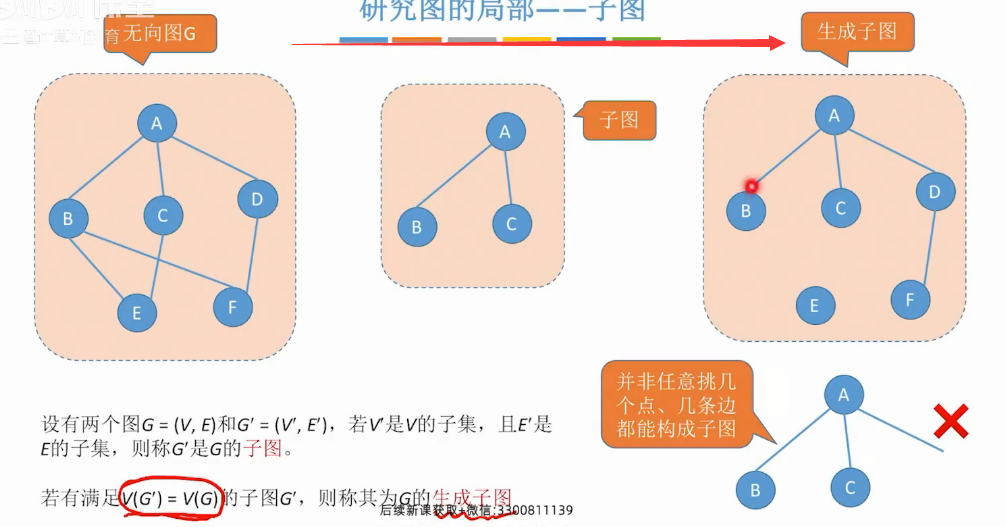
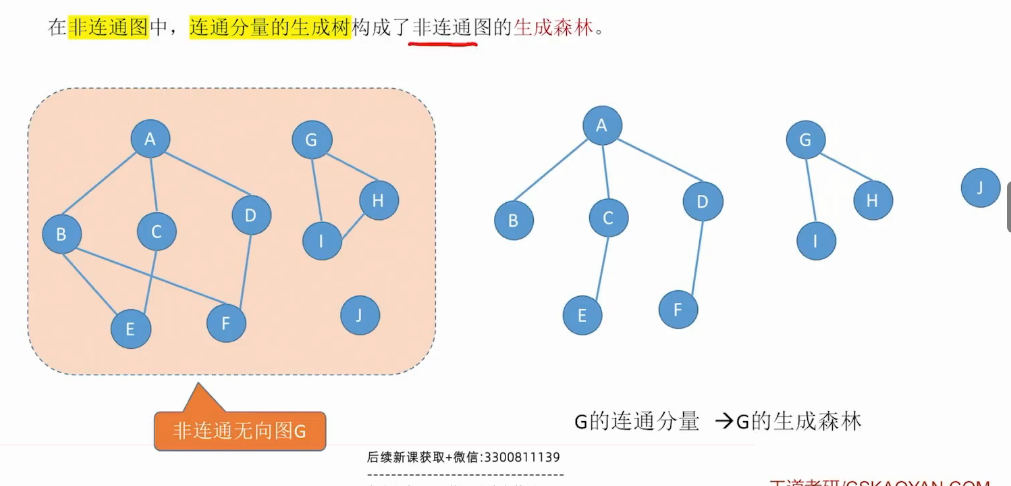
连通分量

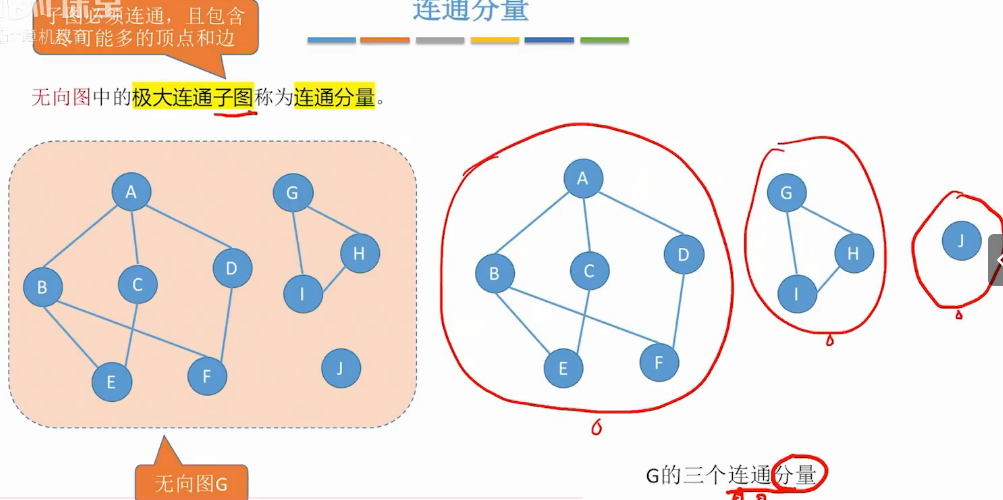
现实意义

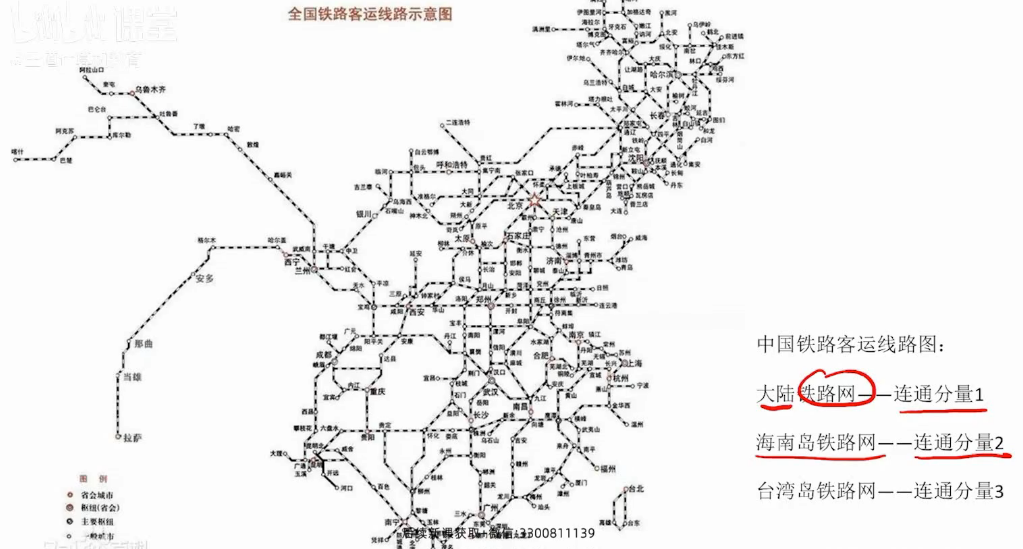
强连通分量

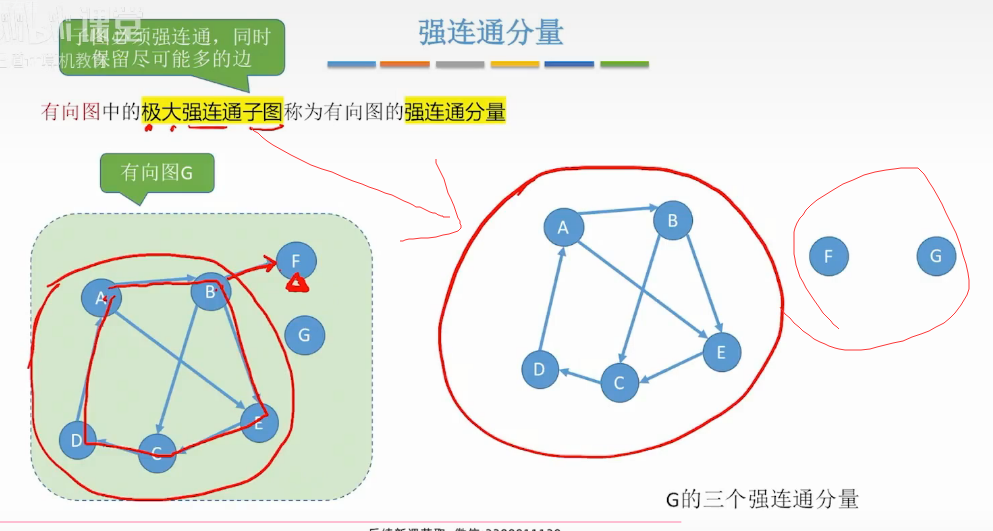
生成树

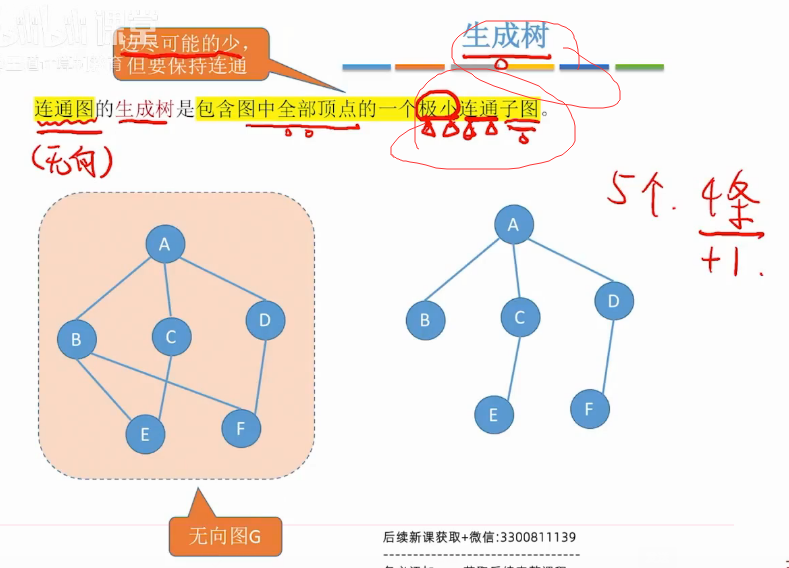
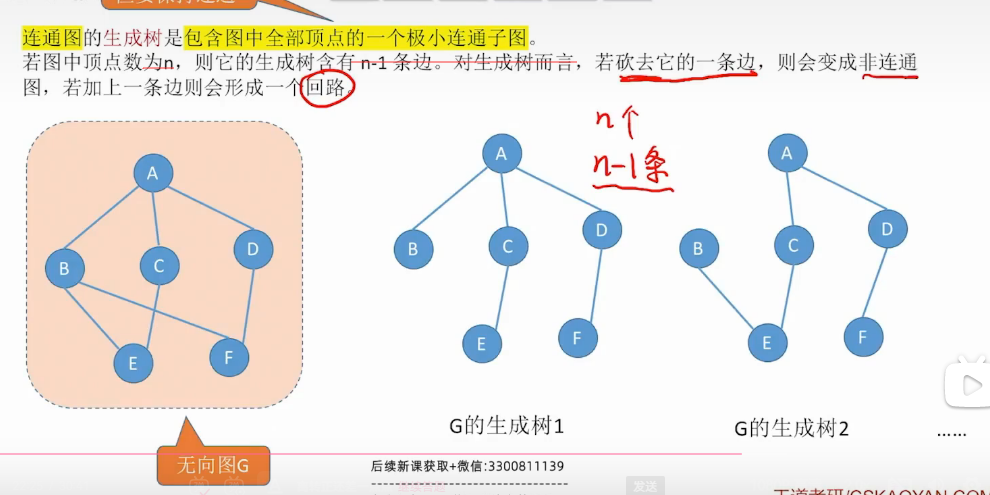
最小的边 生成树–n-1条边

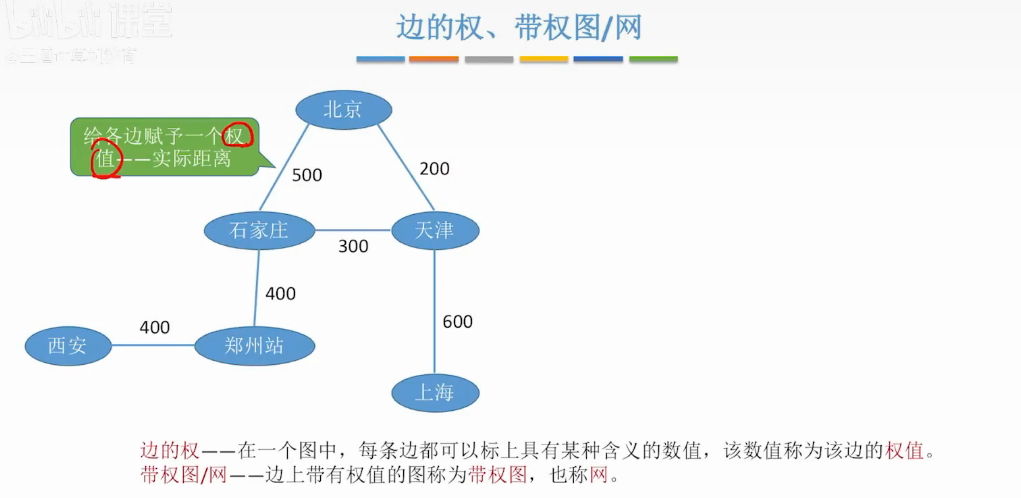
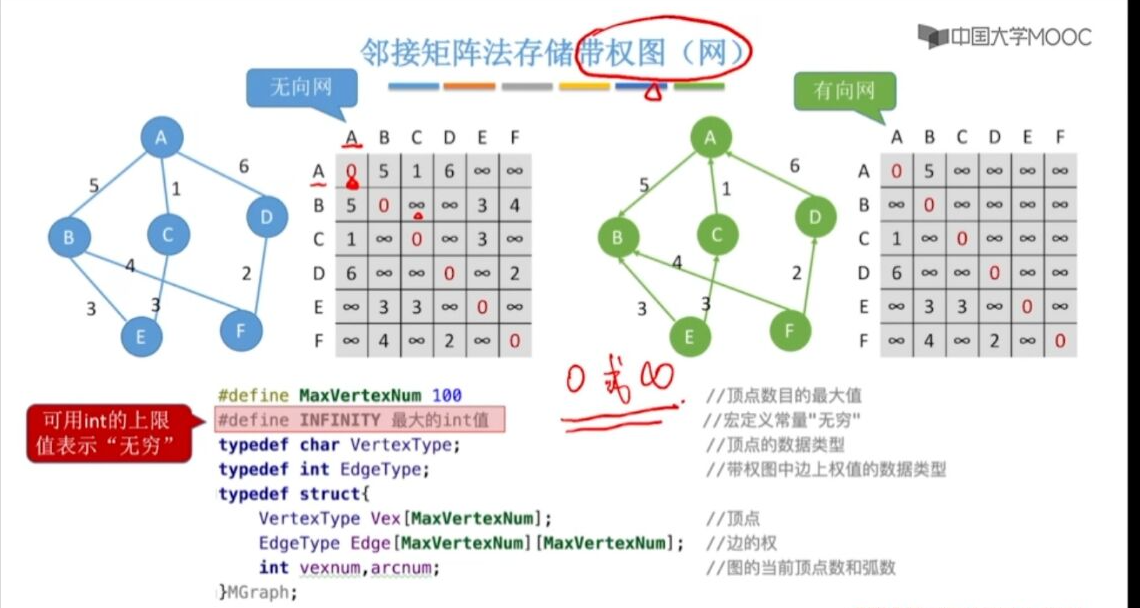
边的权 带权/网

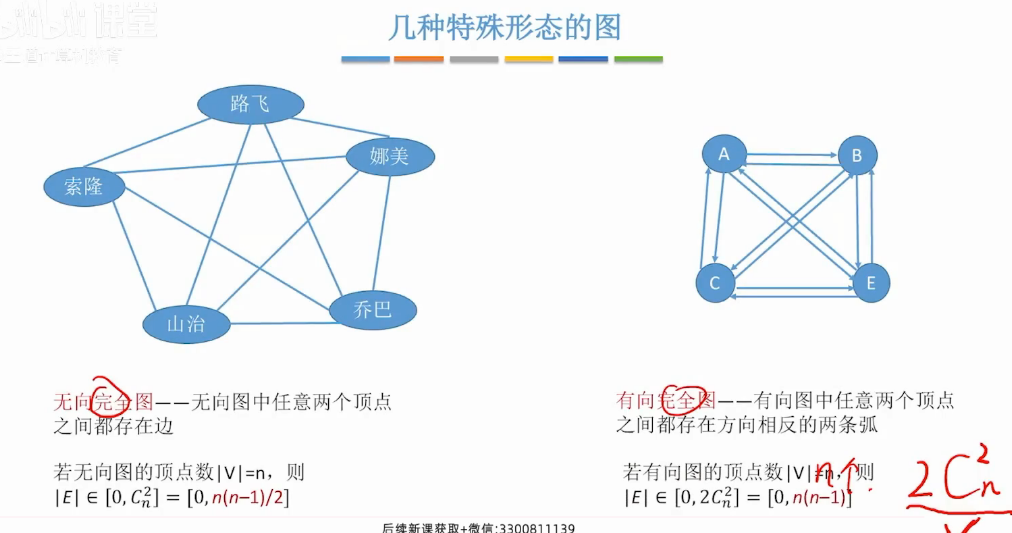
几种特殊的图

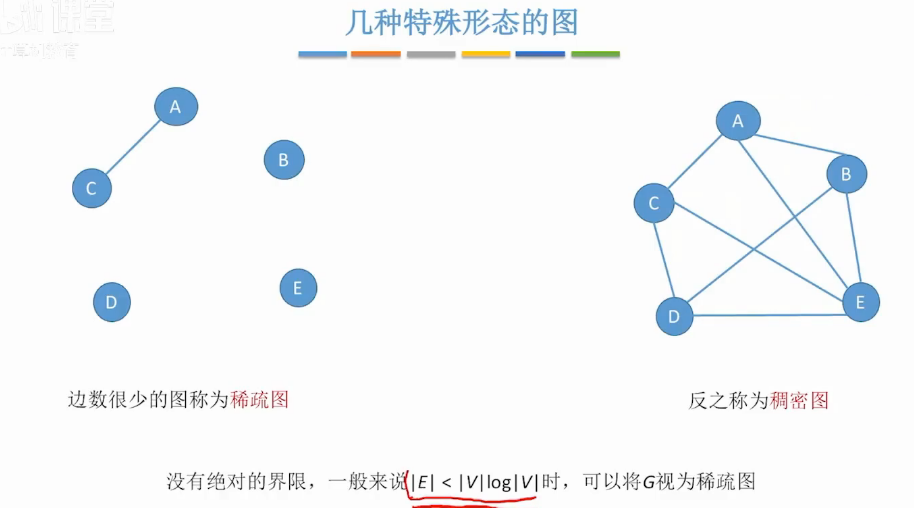
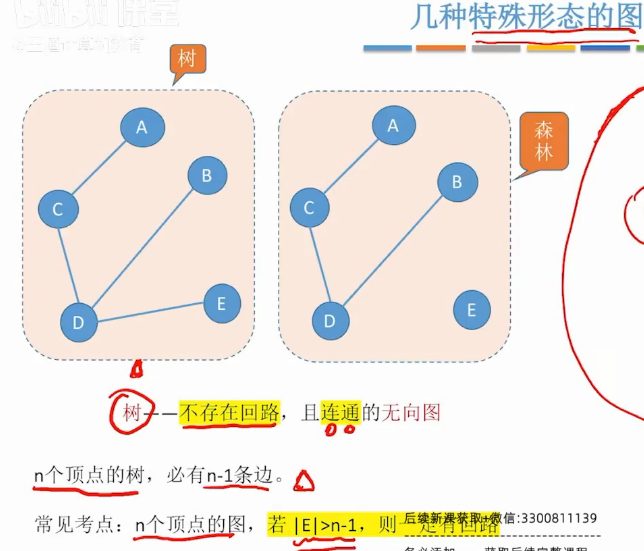
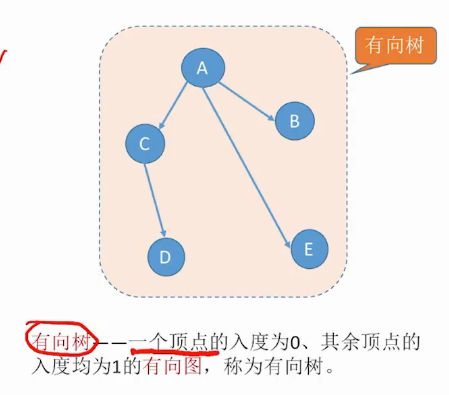
总结

邻接矩阵法-图

---

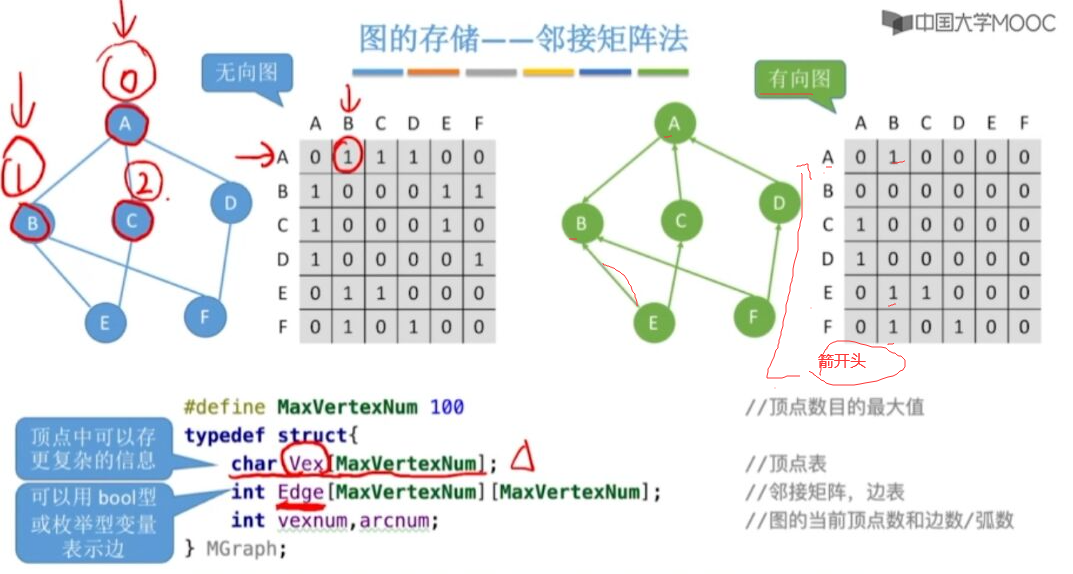
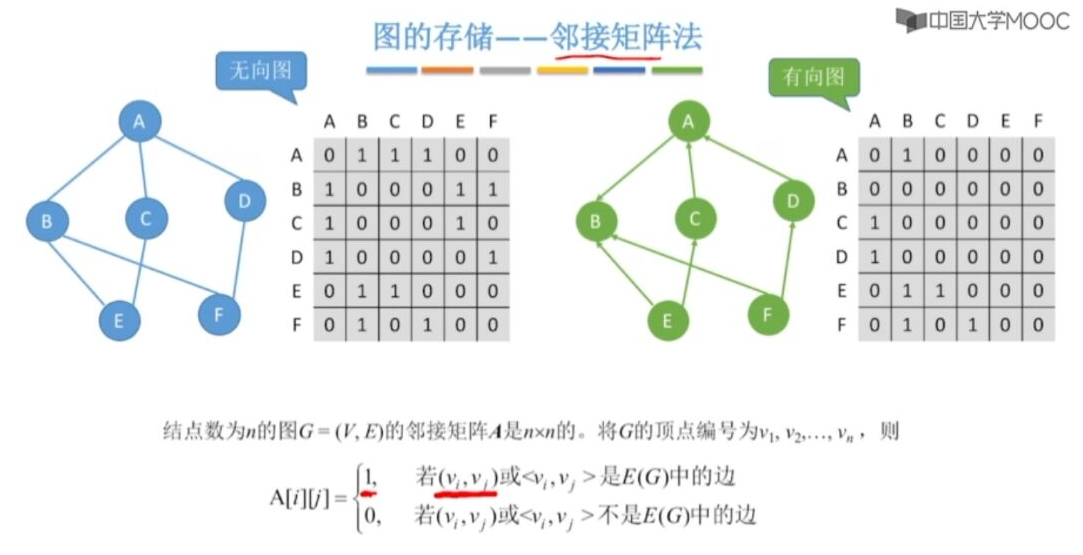
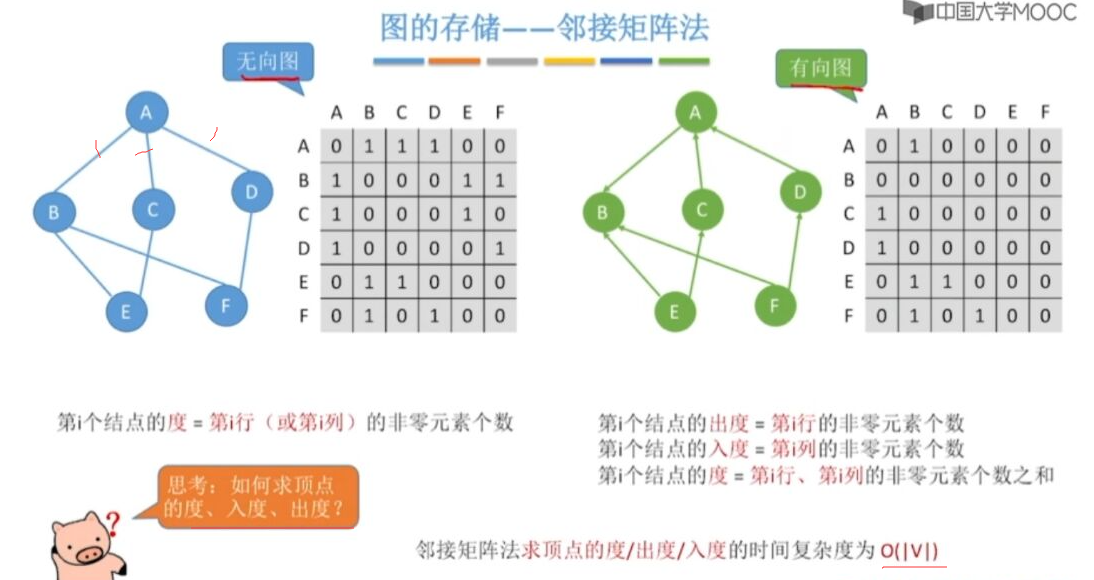
度的计算

带权图

性能分析

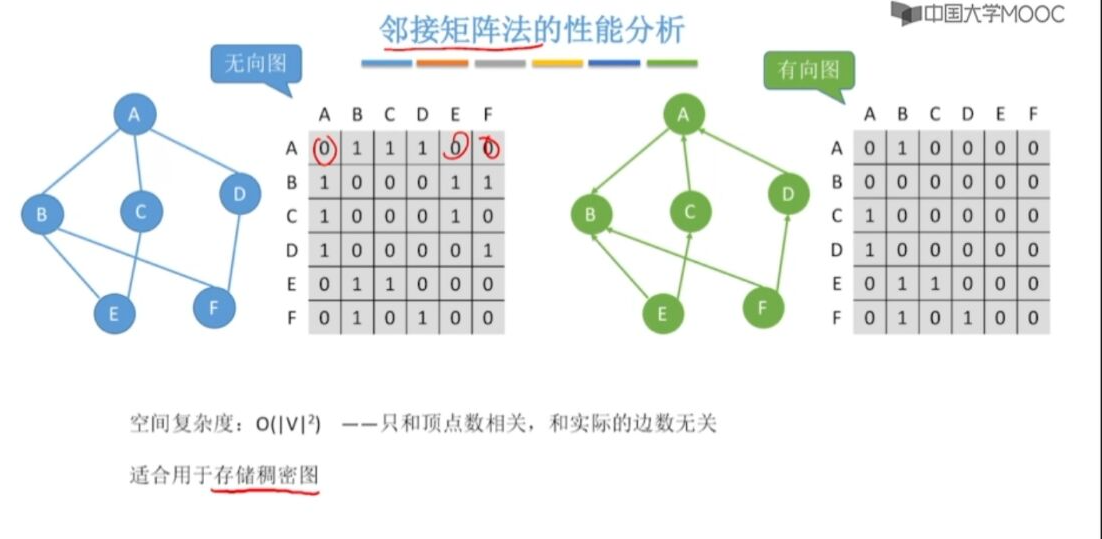
性质-路径计算

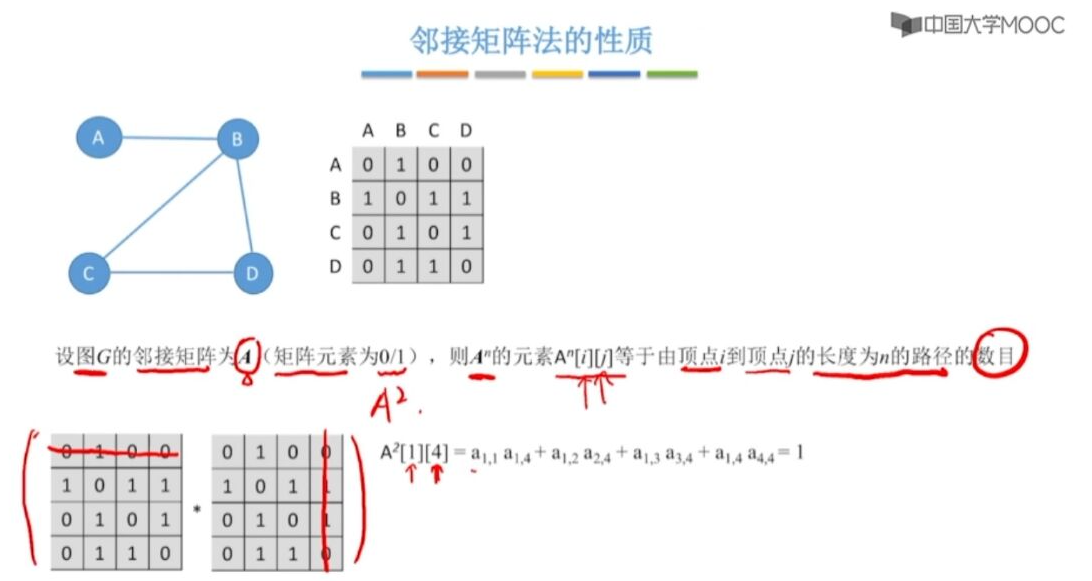
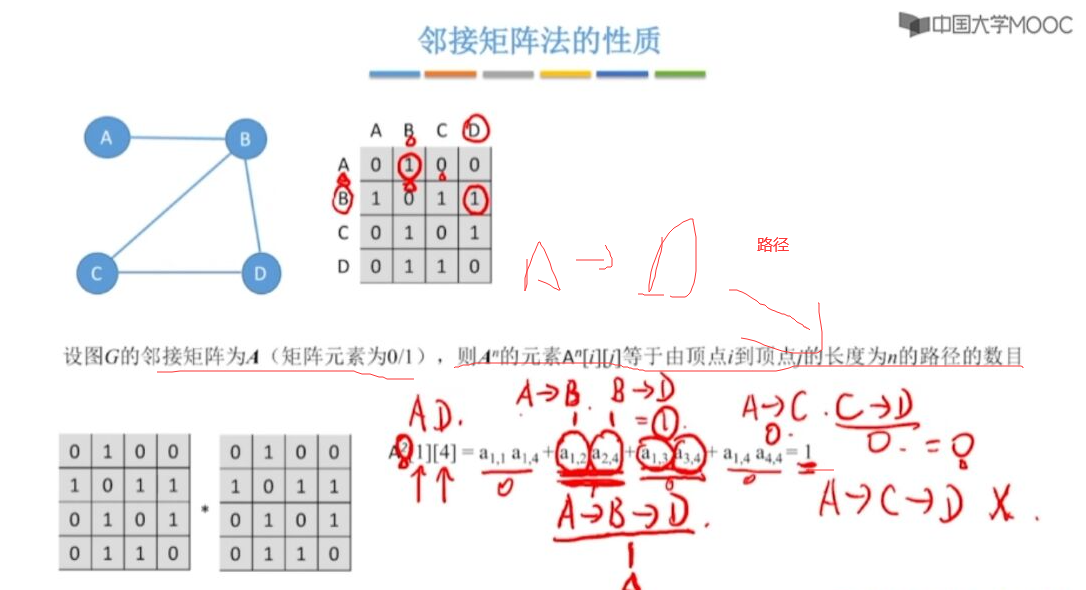
人为计算出-由A->D有多少条路径-比如上图A->D 只有一条

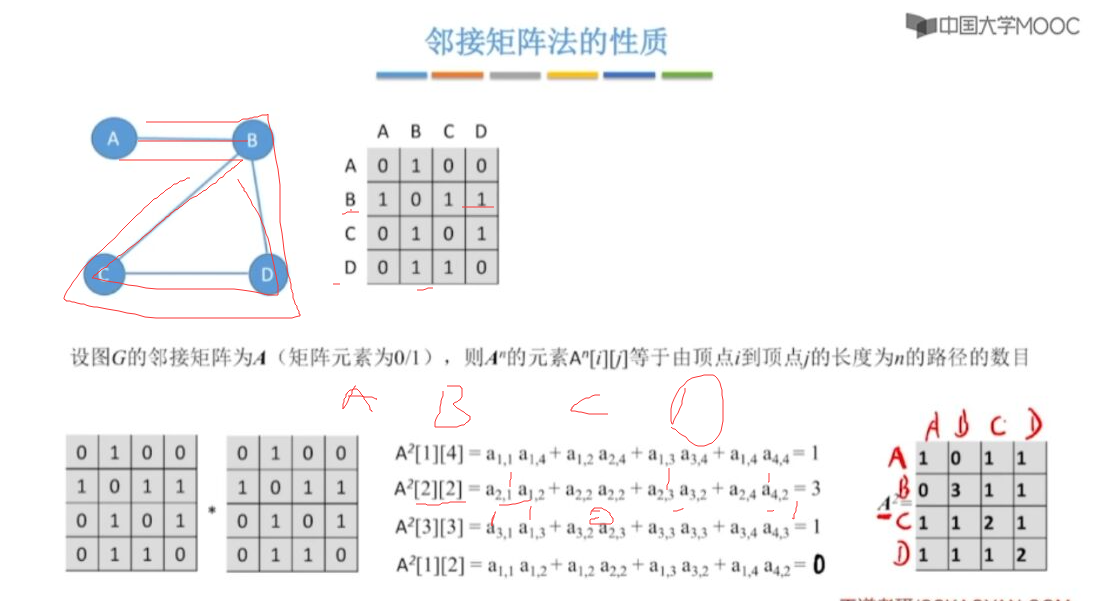
考点回顾

邻接表法

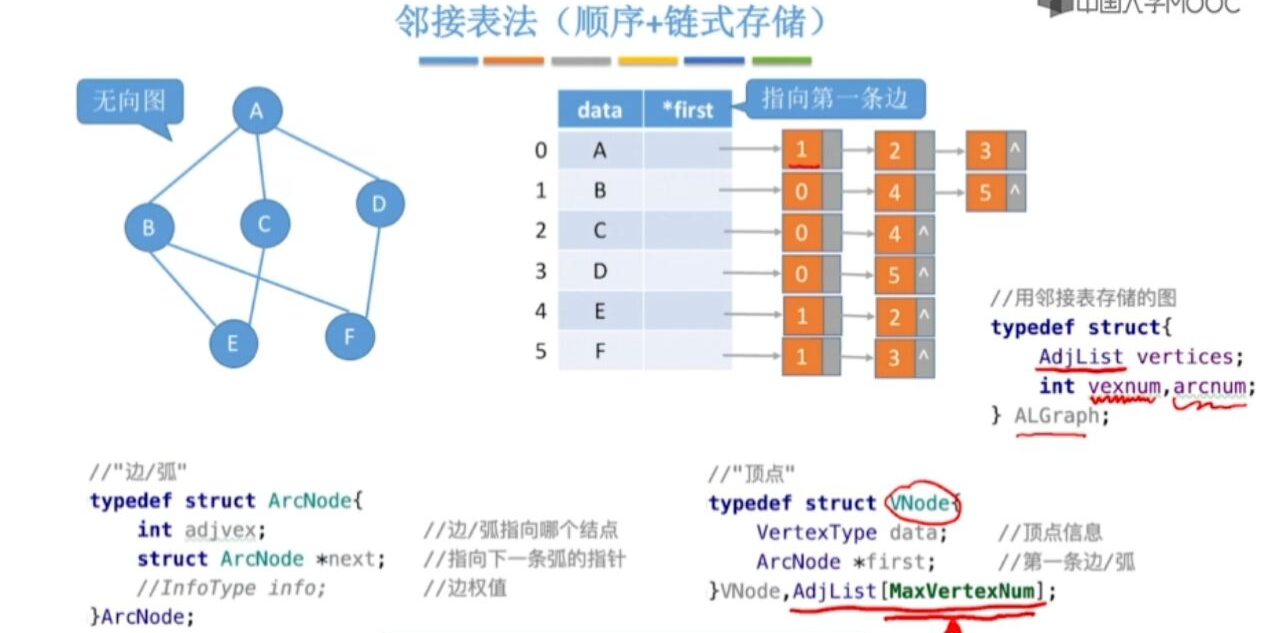
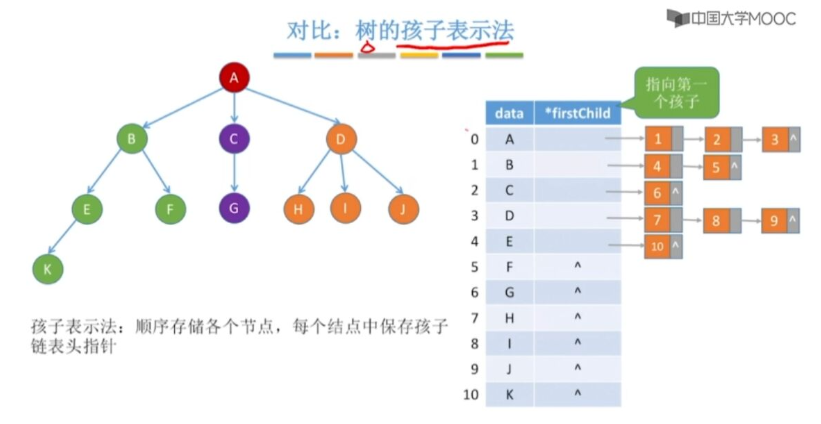
1.出入度计算

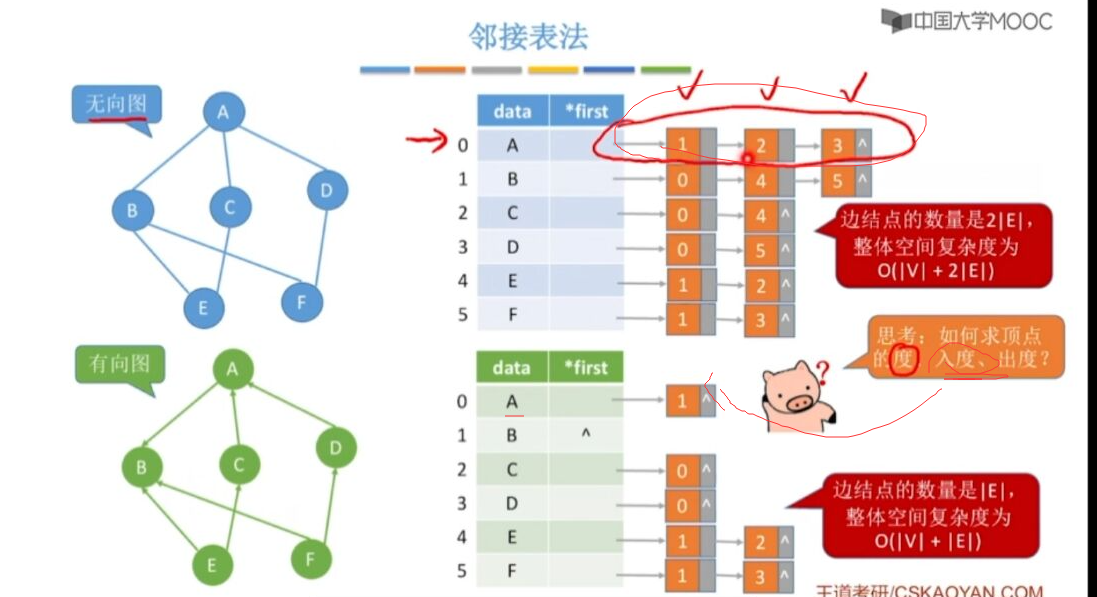
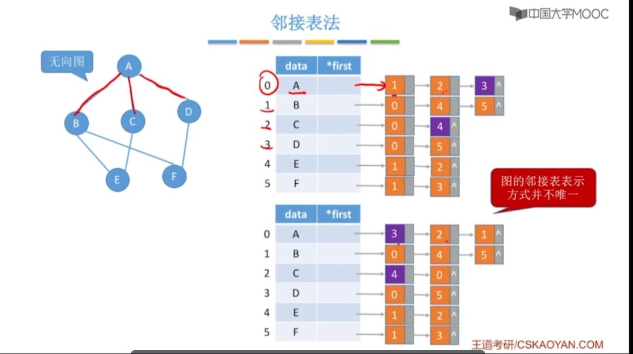
对比

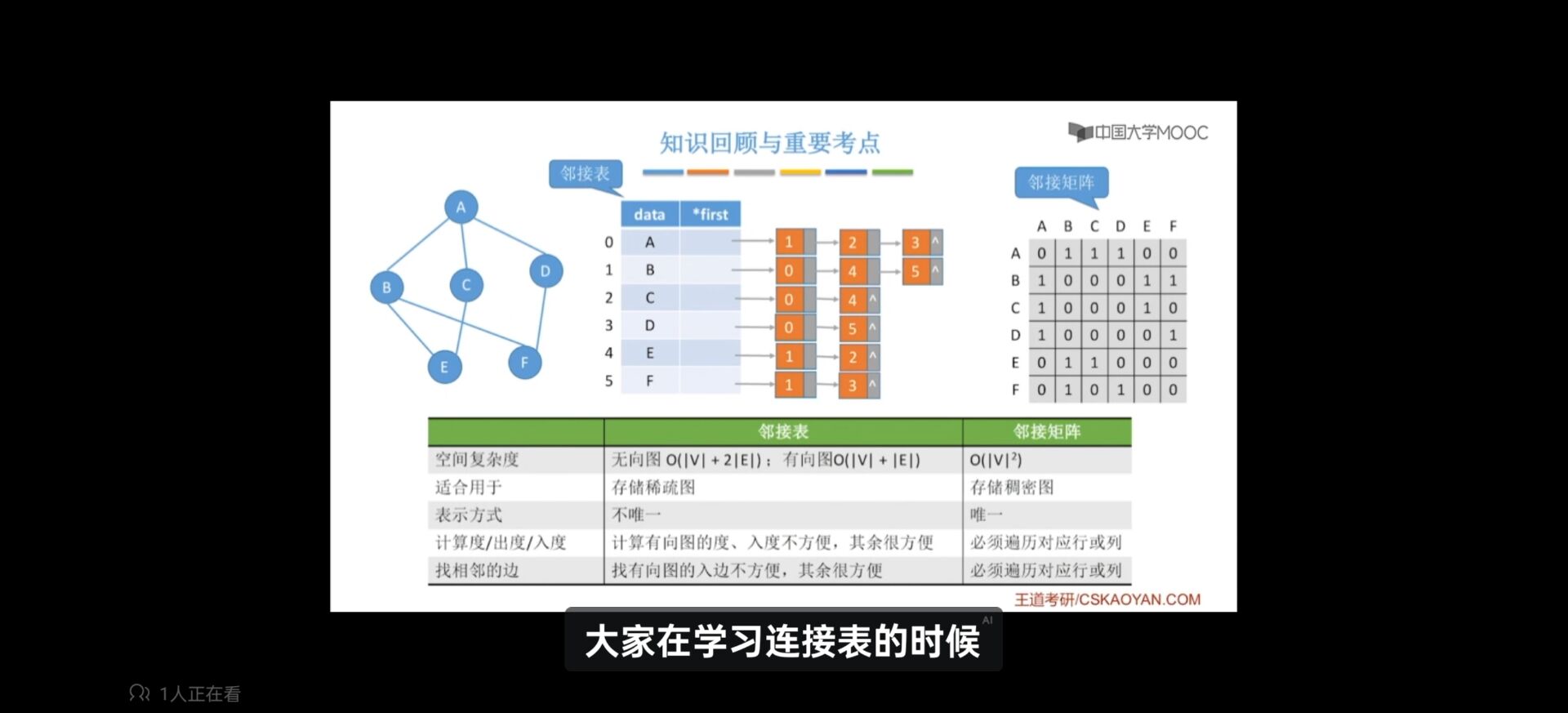
图的遍历

图的定义

深度优先搜索

先序-根左右

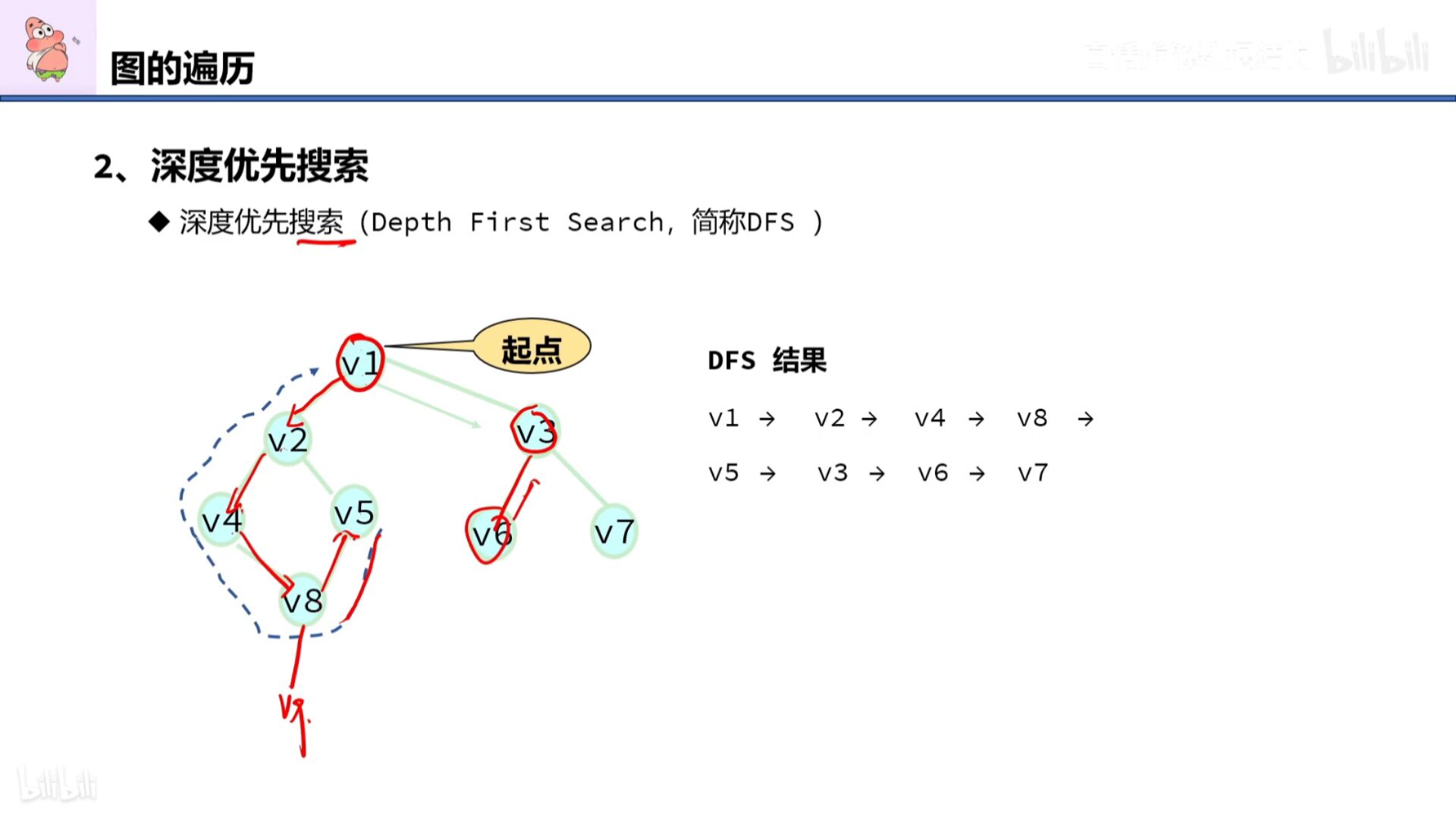
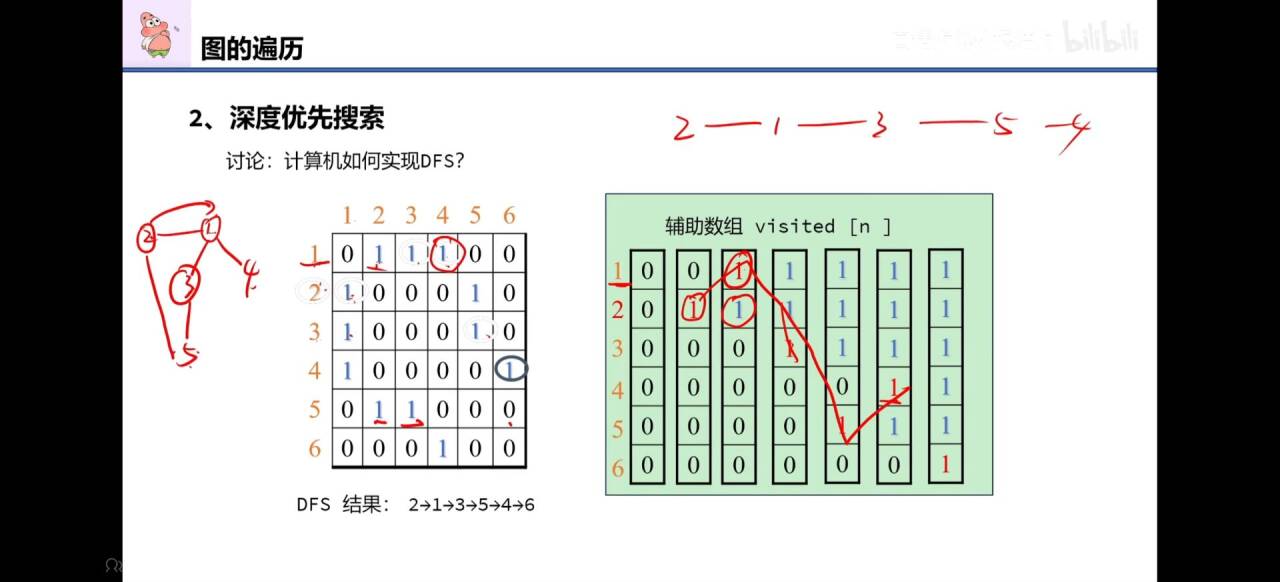
计算机实现dfs

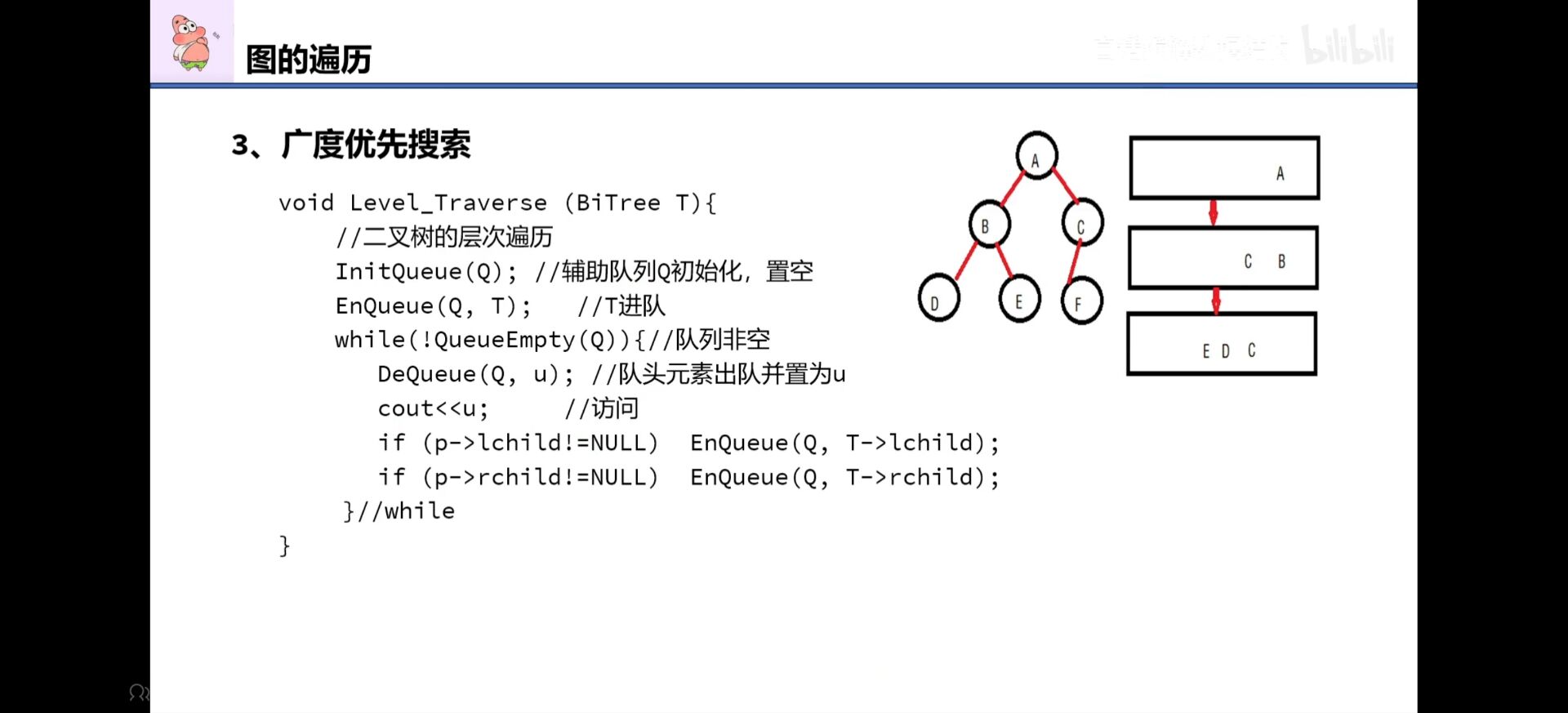
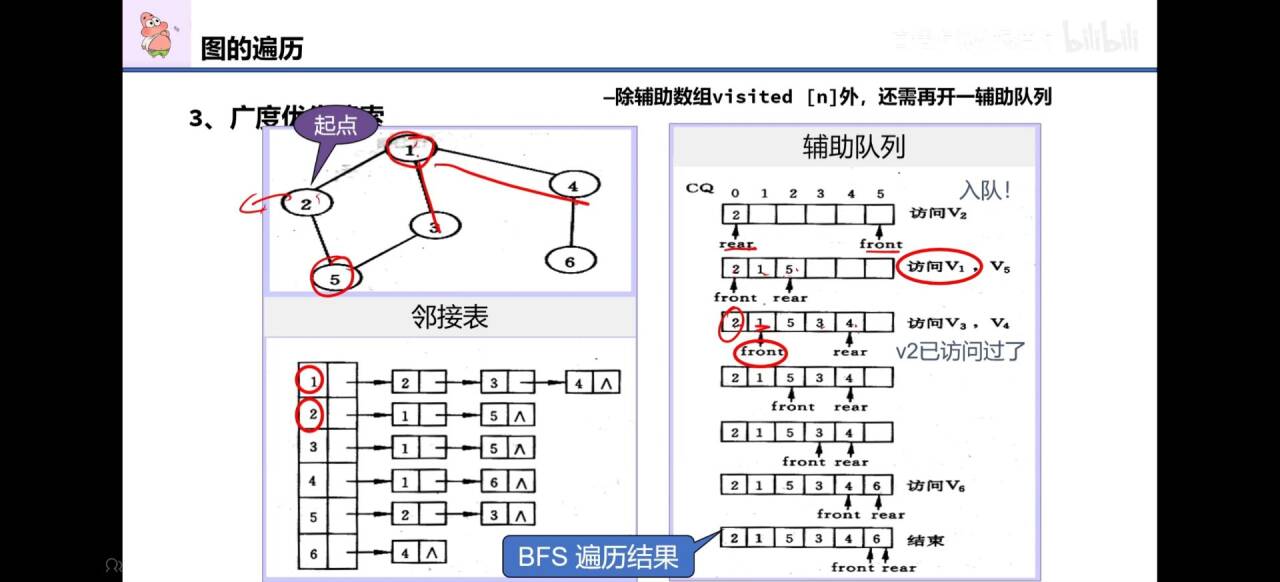
广度优先算法

层次遍历

最小生成树

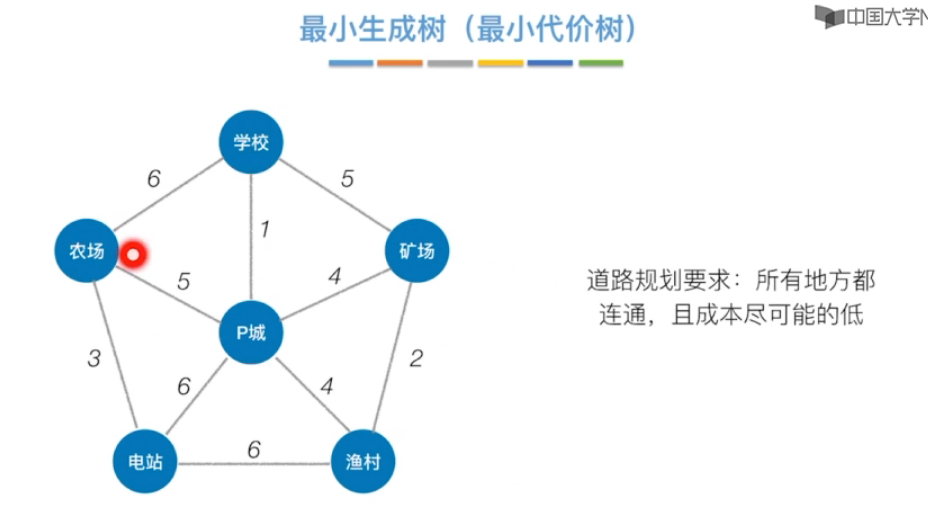
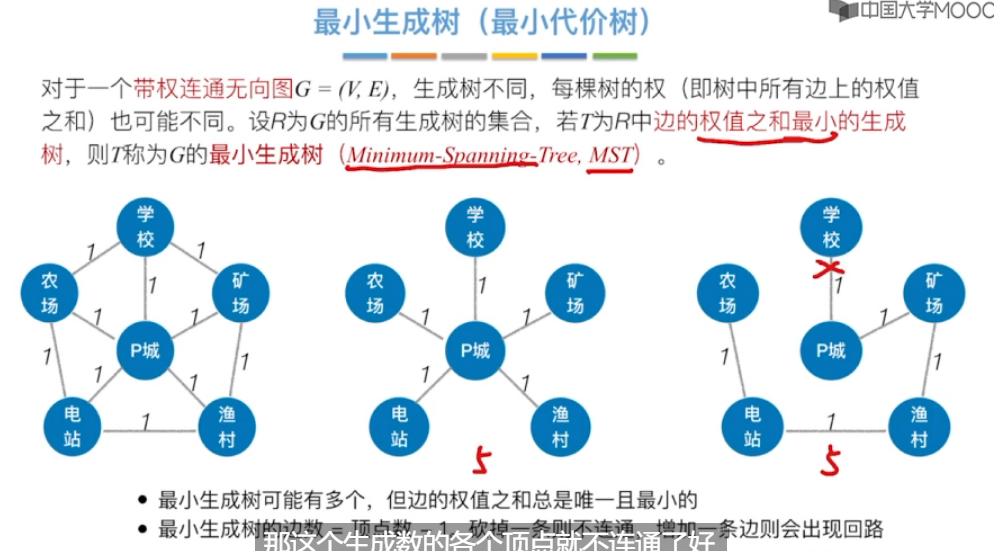
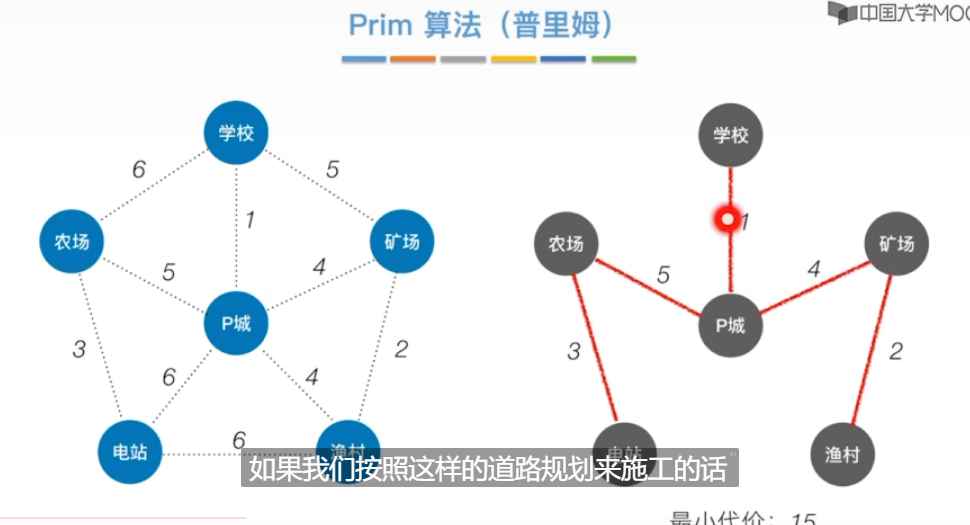
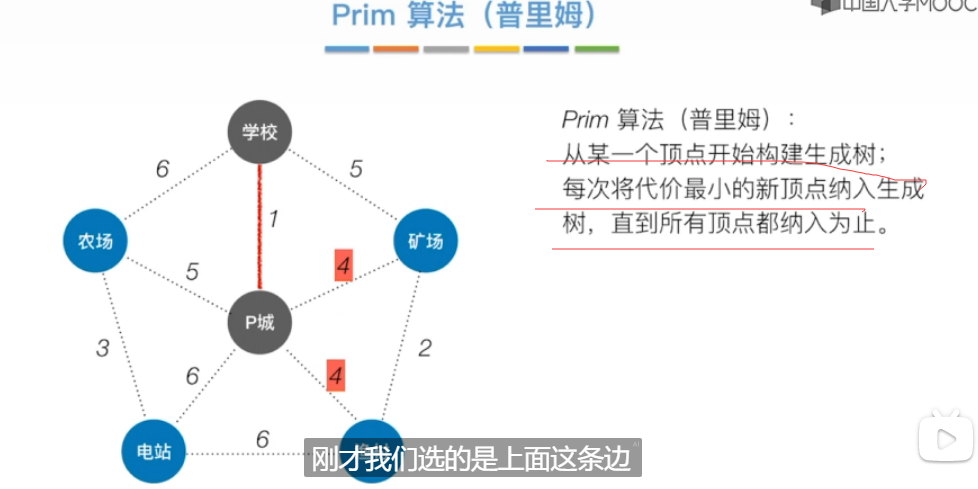
普利姆算法

最小生成树-考研阶段补考-我专本贯通不可能考
了解即可

克鲁斯卡尔算法

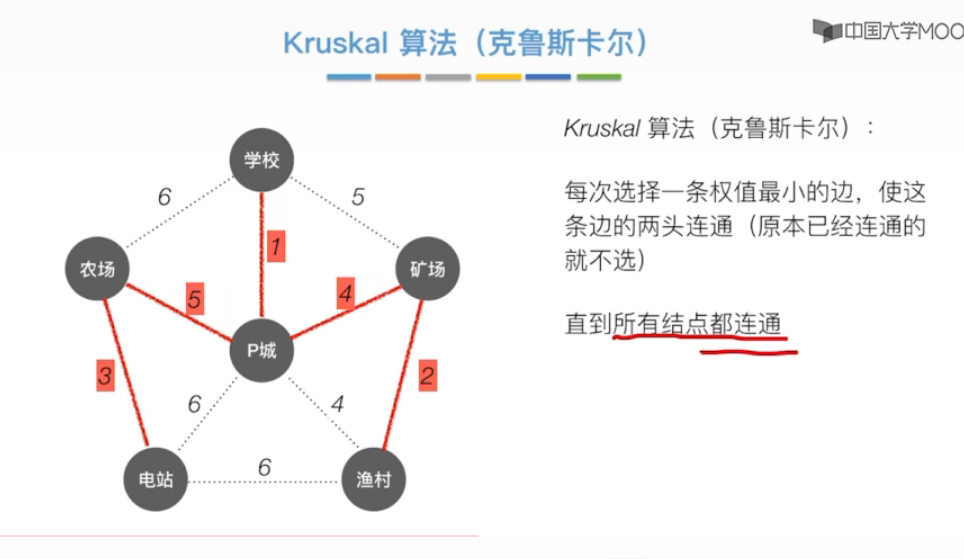
对比

总结