树

6.1.1 树的定义

6.1.1.1树的概念

树是一种非线性结构,它由节点和边组成。节点之间通过边连接.
由n(n>=o)个节点的有限集。n=0表示空树

n>1时满足:
1.有且只有一个根结点并在最顶层

2.其余结点分成互不相交的 M 个子集,每个子集又是一颗树。

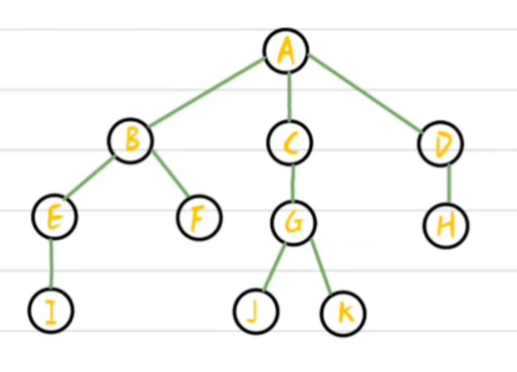
案例

6.1.2 树的逻辑结构表示

6.1.3 树的基本术语

6.2

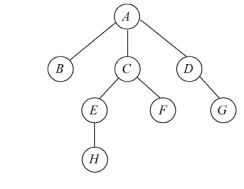
1234 探讨的是节点的度

节点位置探讨 5 6->对套

抽象节点 7 ->包括孩子和孙子

8 _>H E C A 只要能找到对应父节点就继续

9 父节点下 同分支下-兄弟节点(节点层次相同 )

10 树的高度

11

6.1.4 树的性质

1.树的节点数

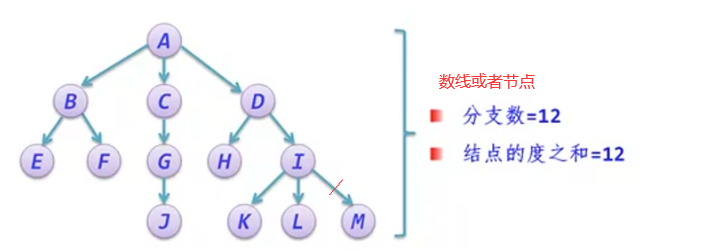
节点数=总度数(数线或者自己遍历)+1

例如 A的度数 2 B C1 G 1省 3+2+1+1+2+3=12-再加上A-就是总度数

2.度为m的数第i层至多节点

3.高度为h m次树至多有多少个节点

例如高度4 -3次树

“m 次树”指的是 每个节点的度最多为 m 的树，即每个节点最多可以有 m 个子节点。

333*3=81-1=80/2=40

手算

A(3) 9 - 9*3=27 -27+9+1=37+BCD =40手算也能对上

6.1.5 树的基本运算

1.树的运算

2.树的遍历

6.1.6树的存储结构

计算机中-树存储着节点的值-还有节点与节点间的关系

1.双亲存储结构

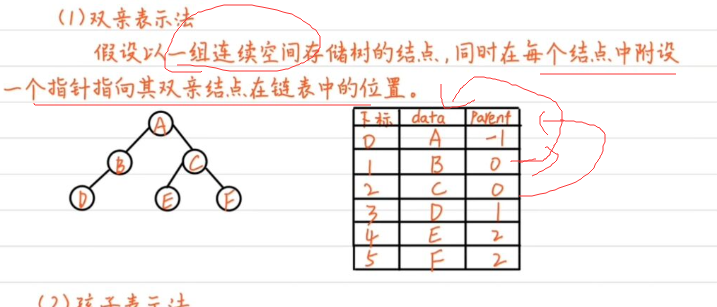
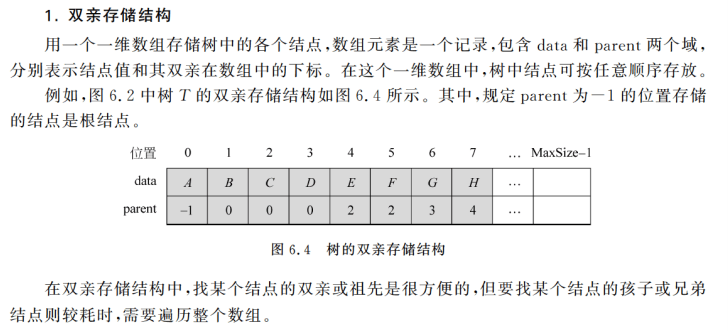
2.孩子链表存储结构

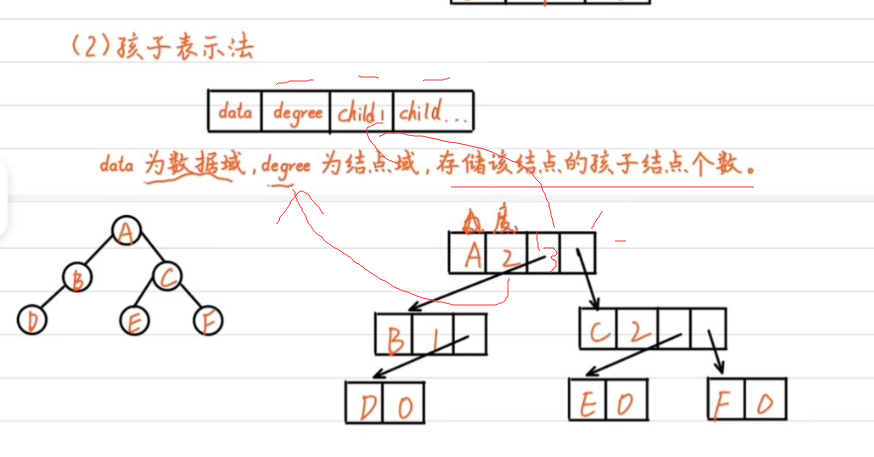
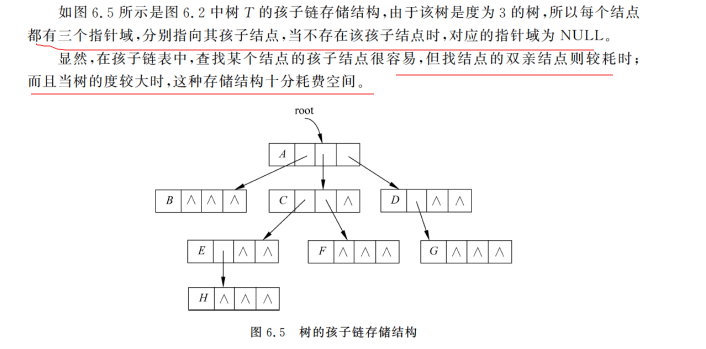
用空间换来部分算法遍历

3.孩子兄弟表示法

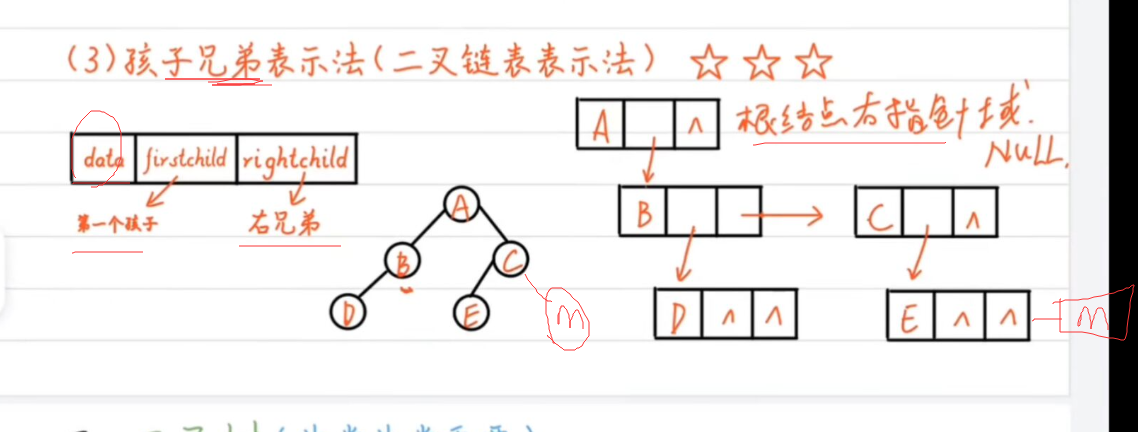
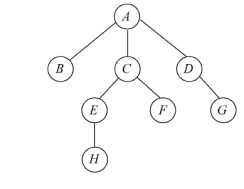
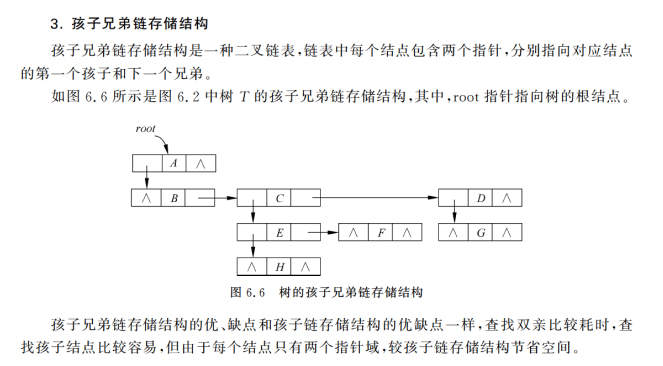
二叉树

二叉树的每个节点最多只有2个后继节点，度最大为2

6.2.1二叉树的定义

逻辑表示

注意“二叉树是度为2 的树”这句话是错的，二叉树可能度为0，度为1或者度为2，所以二叉树的度≤2

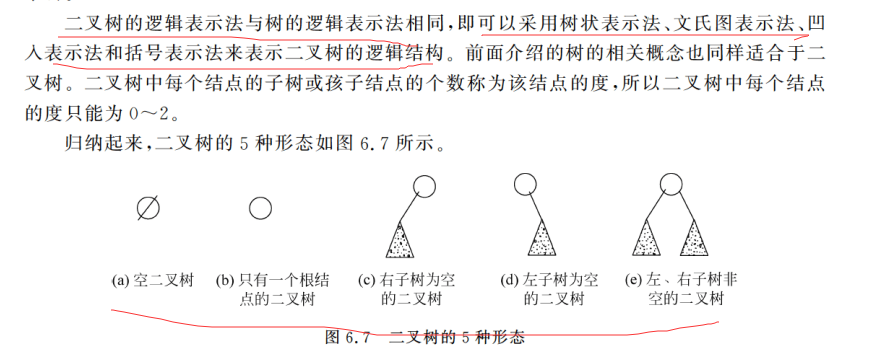
例

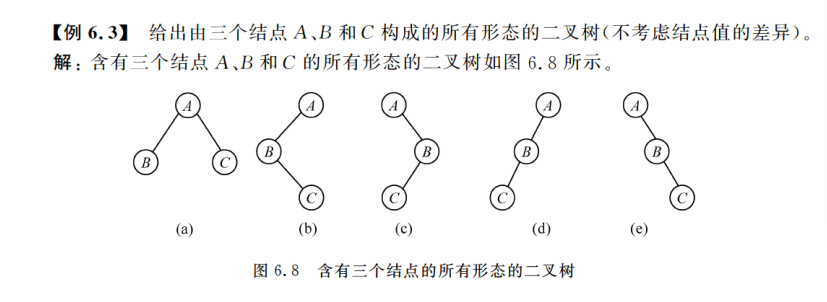
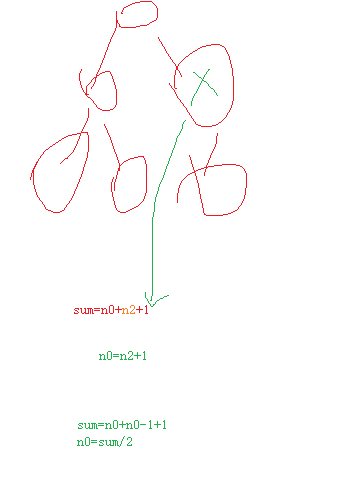
6.2.2 二叉树的性质

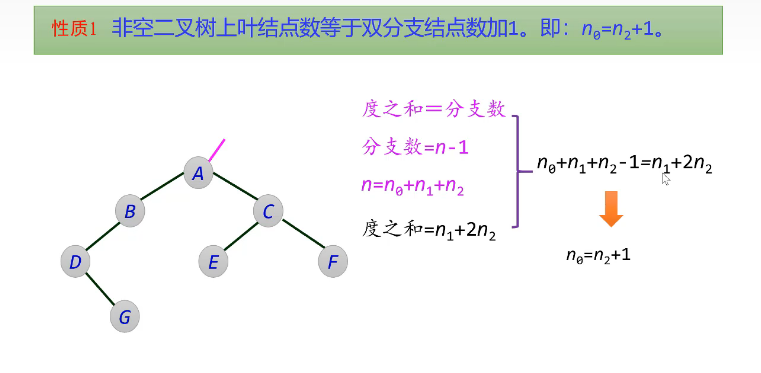
n 0->叶子节点个数–

n2-是度=2的节点个数

C

特殊二叉树

1.斜树

2.满二叉树

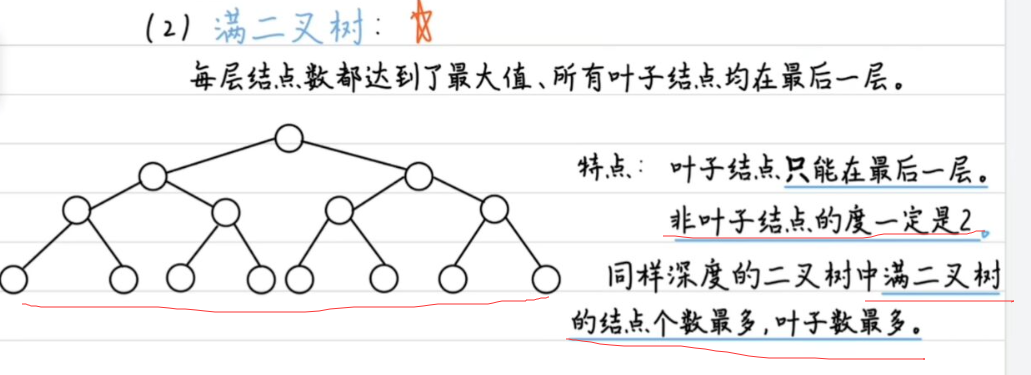
高度为h–2h次方-1 -节点最多的情况

计算节点最多情况-

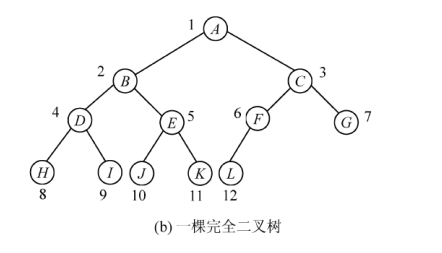
3.完全二叉树

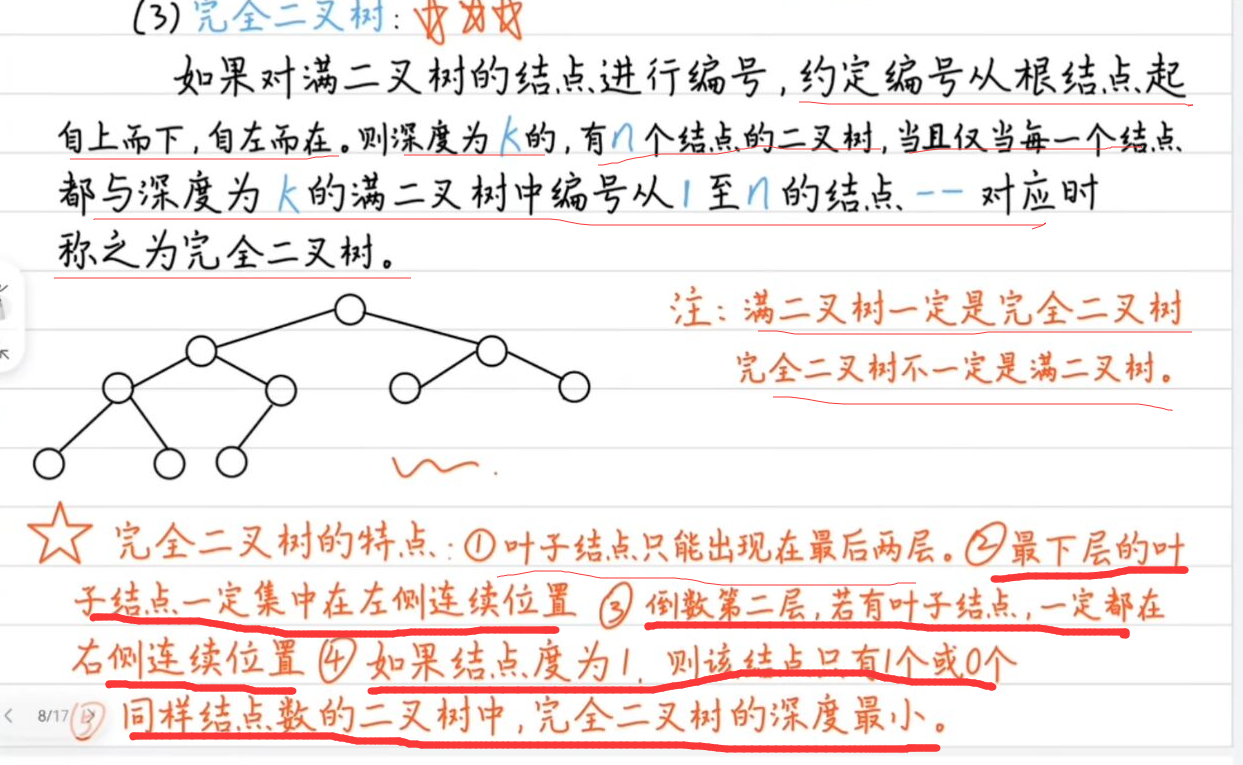
完全二叉树特性

完全二叉树实际上-对应的是满二叉树删除叶节点最右边若干个节点得到的

二叉树中至多只有最下边两层节点的读书小于2 ，并且二叉树中任意一个节点的右子树高度为h.则左子树的高度只能是h或h+1，因此高度为h的完全二叉树若按层次从上到下，从左到右自然数编号，它与高度为h的满二叉树中节点的编号一一对应

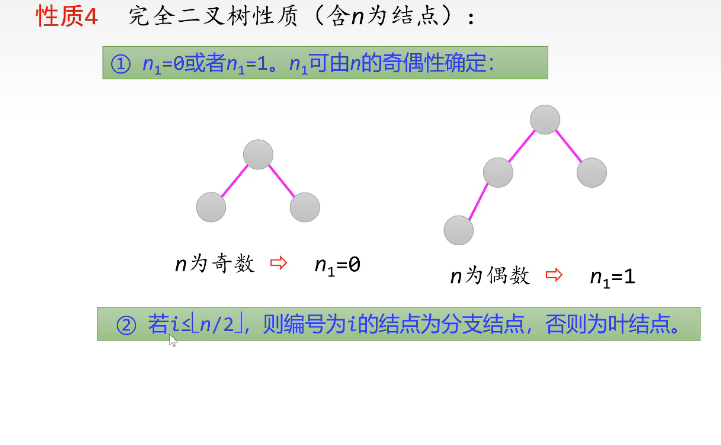
n 1是度为1

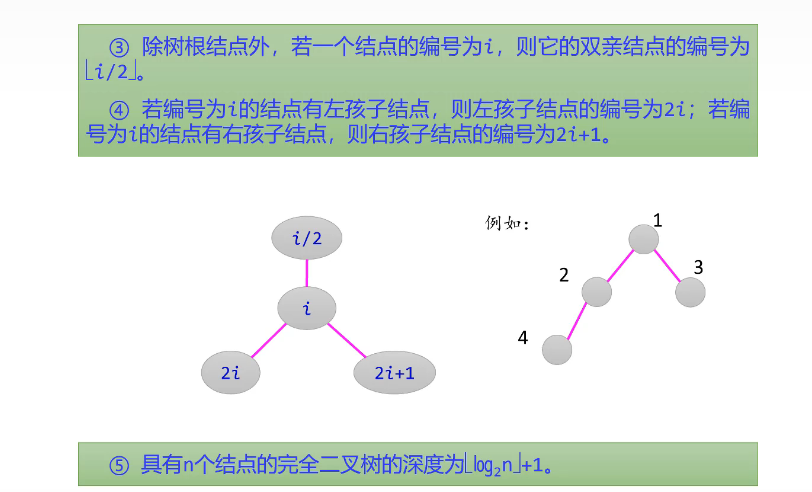
3.1完全二叉树 父节点 左孩 右孩计算

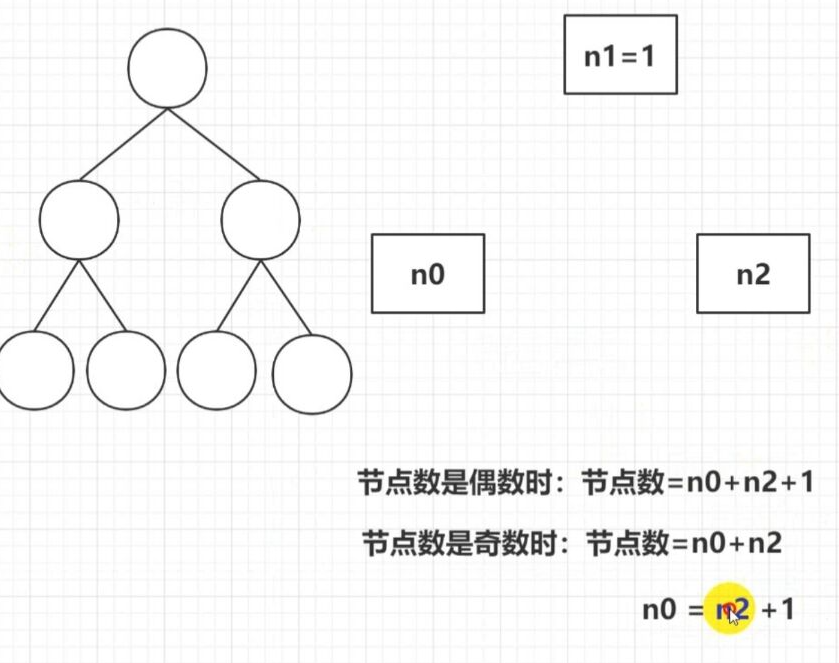
4.完全二叉树叶子节点计算

满二叉树
2 h~1 4
节点书 7=叶子节点+n2

叶子节点=n2+1 度为2的所有节点+1

7=n2+n2+1=2n=
n=3

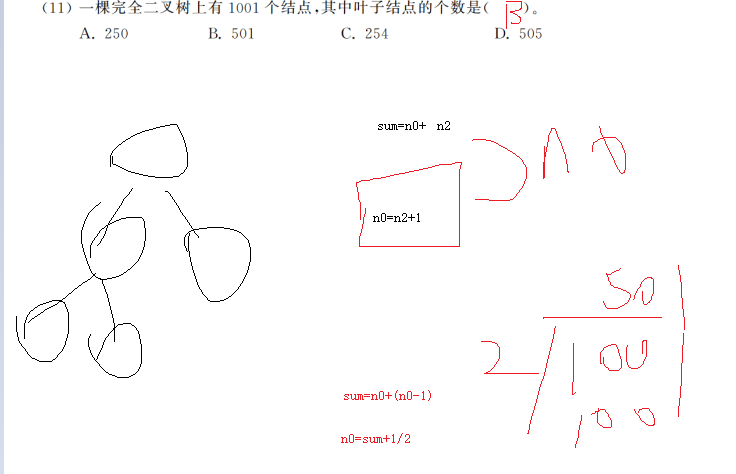
偶数情况

6.2.3 二叉树的存储结构

二叉树的顺序存储结构

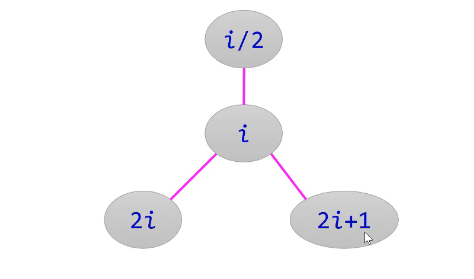
双亲就是节点I/2=双亲

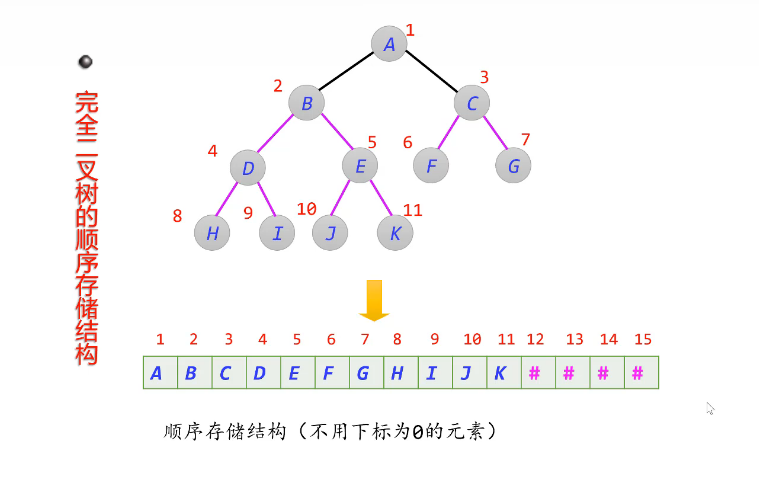
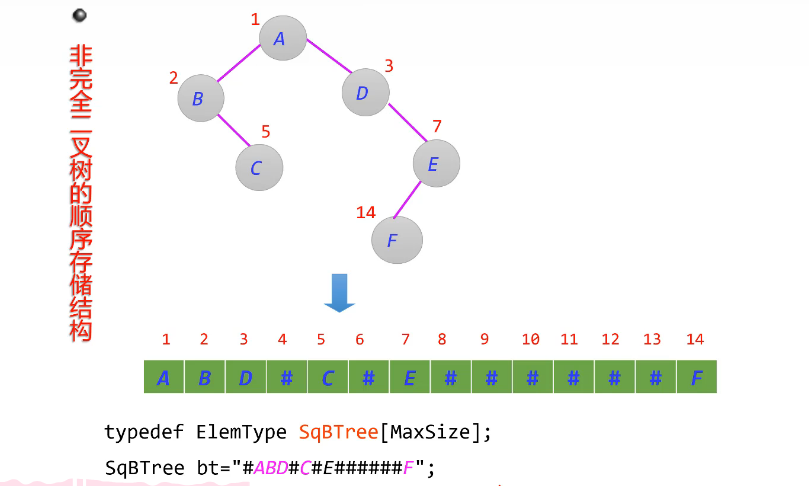
可以先画满的再自己擦除

具有空间浪费
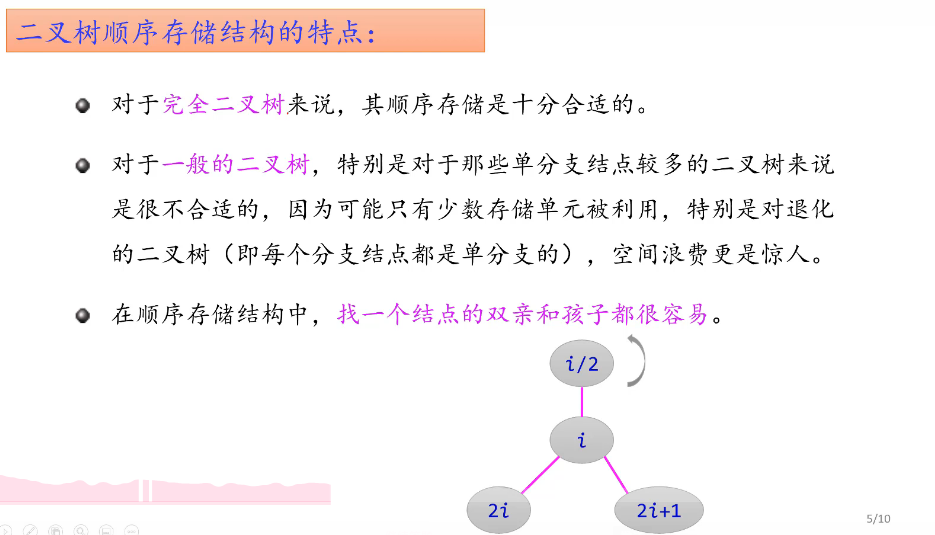
特点总结

二叉树的链式存储结构

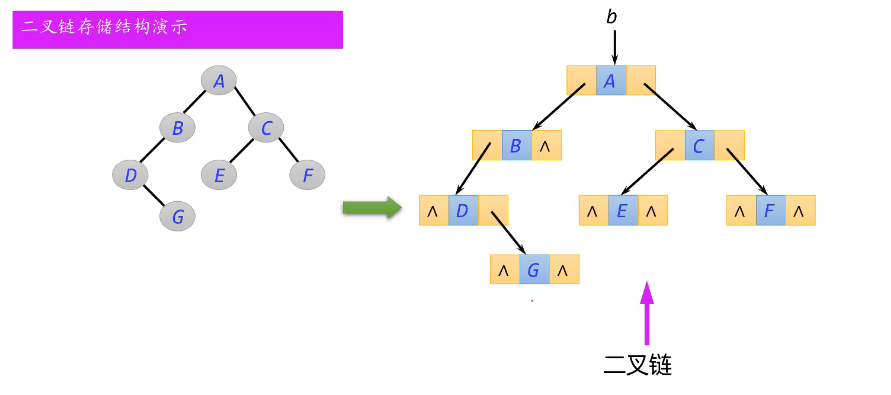
叶子节点特点-左右都为空
左 数据 右

二叉树特点

—找双亲不方便 可以写三链式表

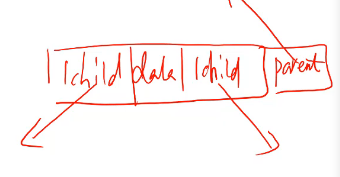
存储双亲链

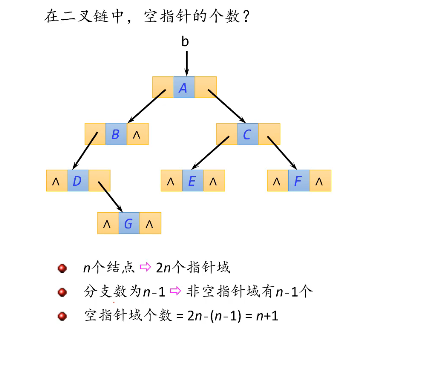
6.2.4 递归算法设计

1.递归算法了解

递归模型 递归出口-递归的终止条件 递归体 递归求解的递推关系

2.二叉树的递归算法设计

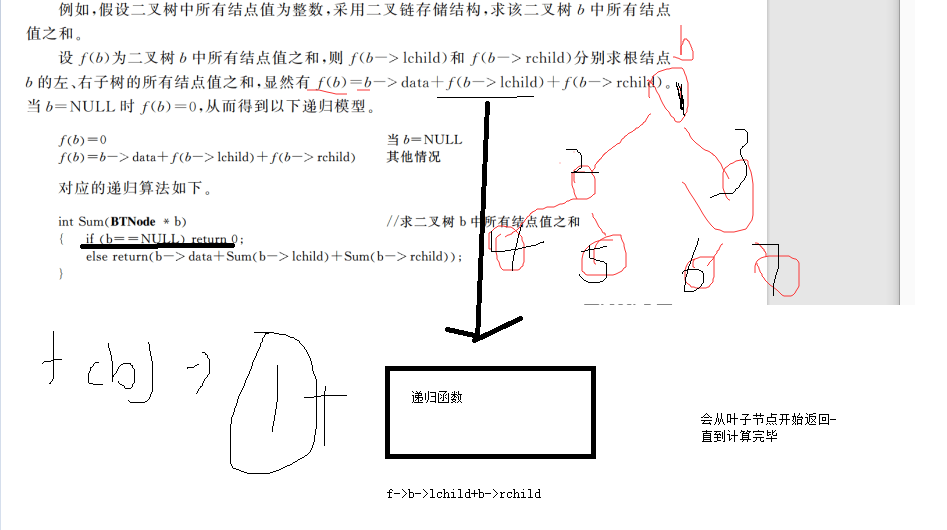
整个递归过程的关键在于，从树的最底层（叶节点）开始计算，每次计算当前节点的值并将结果返回给上一层，最终返回根节点的总和。图中箭头所示就是递归函数从叶节点向上返回的过程。

这个递归实现了树的后序遍历（左子树 -> 右子树 -> 根节点），每个节点都只被访问一次，因此时间复杂度为 O(n)，其中 n 是树中节点的总数。

6.4二叉树的基本运算

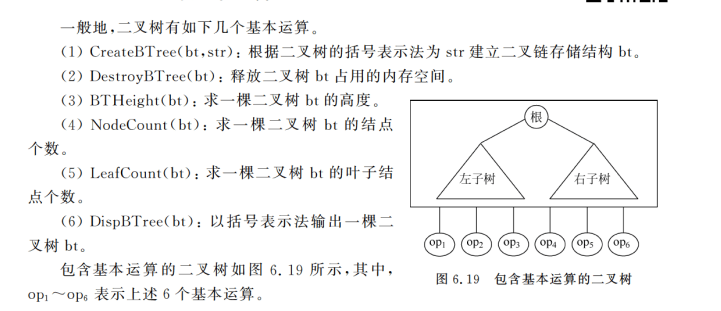
1.二叉树初始化

通过字符来规范树的结构-读取字符进行处理二叉树

2.销毁二叉树

递归算法-结束条件结束bt==null

jhs

3.高度计算

f(bt)=0; bt=null

max(f(bt->lchild),f(bt->rchild))+1;//遍历左右子树-谁高就是谁大

递归代码

递归结束-左右子树都为空

int BThight(BtNode *&bt)

{

int lchildddep,rchildddep;

if(bt =null) return 0;

else

{

}

}

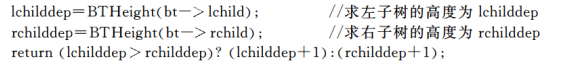
从根节点的左右子树遍历下去-嵌套很深

4.求二叉树个数

5.求二叉树叶子节点个数

6.输出二叉树

6.5二叉树的遍历

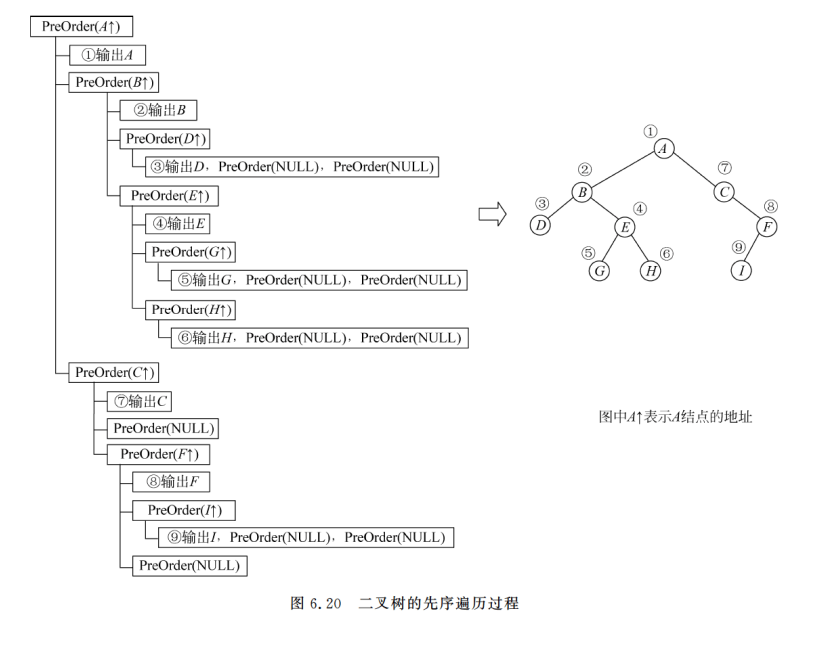
1.前序

若二叉树不为空 -根->左右

递归算法

1
2
3
4
5
6

void pRi(BtNode*ps)
{
//打印
pRi（ps->lchid);
pRi（ps->light);
}

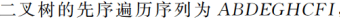
2.中序

左根右

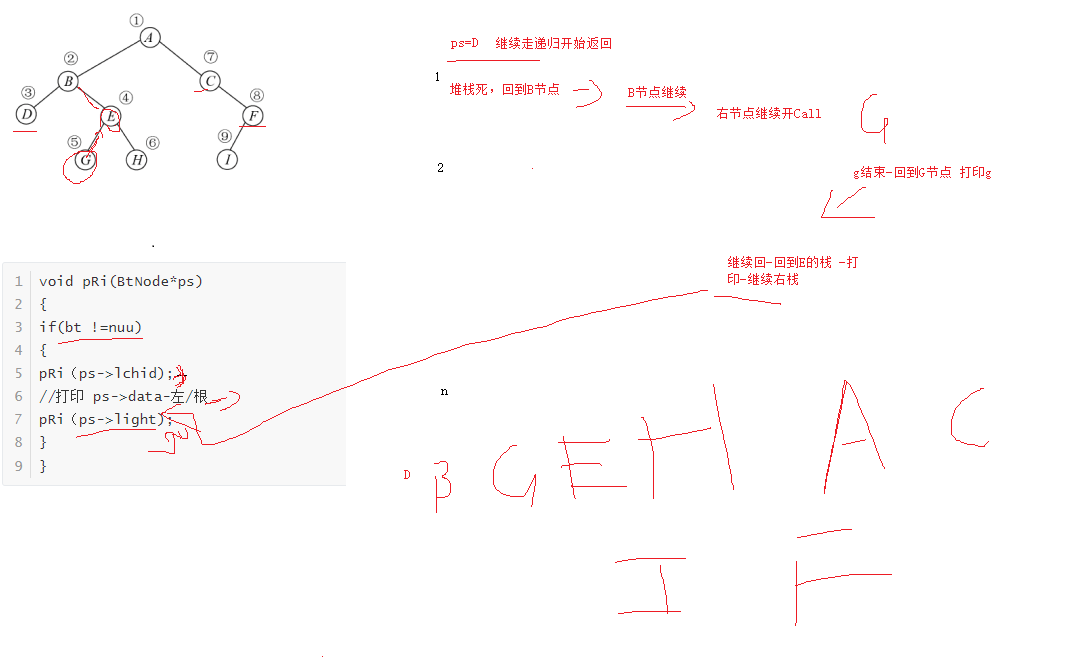
D

3.后序

左右根

4.层次遍历

根节点开始-从上向下-同一层从左到右访问节点

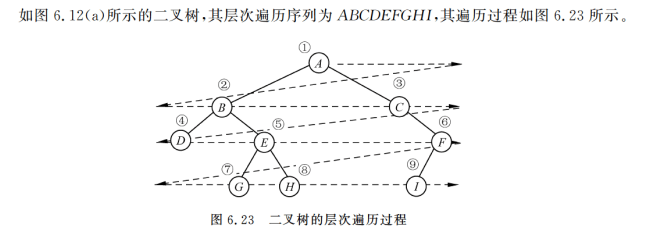
算法剖析

总结

遍历代码

1
2
3
4
5
6
7
8
9
10
11
12

void function(bt )

{
if(bt !=null)
{
//左子树递归

//右子树递归

}

}

前序-中序-后续-的打印结束根据名字来定-考场如果立马思考还是需要时间的

其实依照打印顺序递归也是好想的

序名字-就是根的位置 根左右 左根右 左右 根

6.6二叉树与树的转换

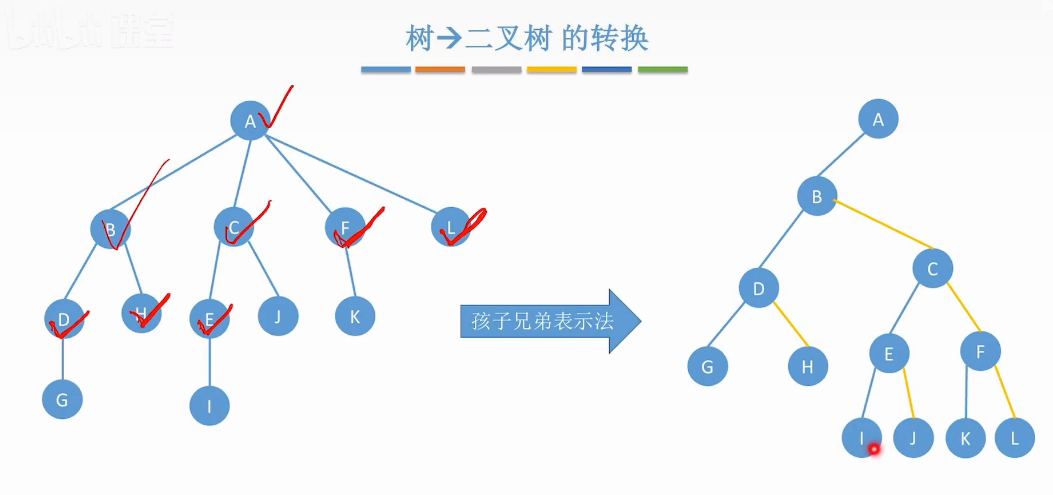
树转换二叉树

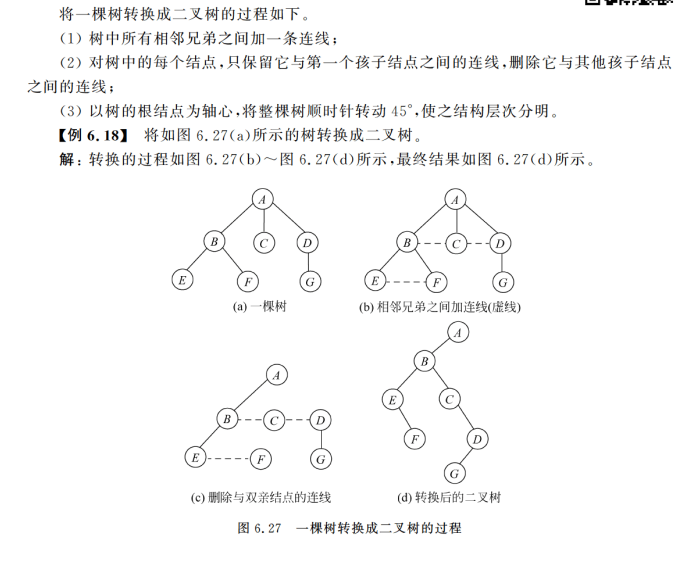
完整步骤-下面是取巧方法

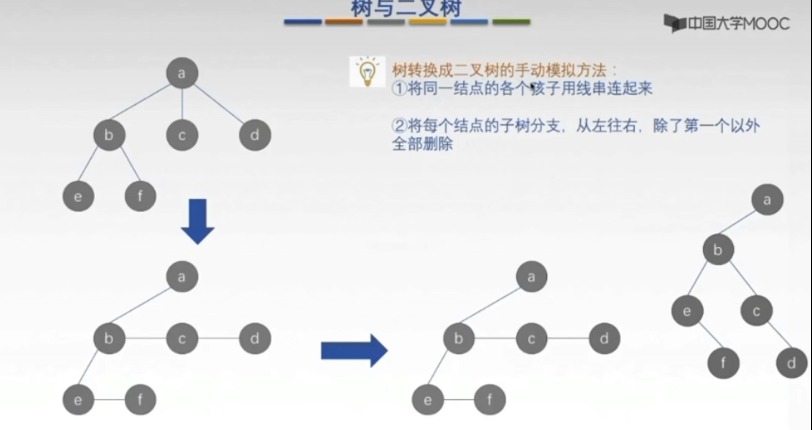
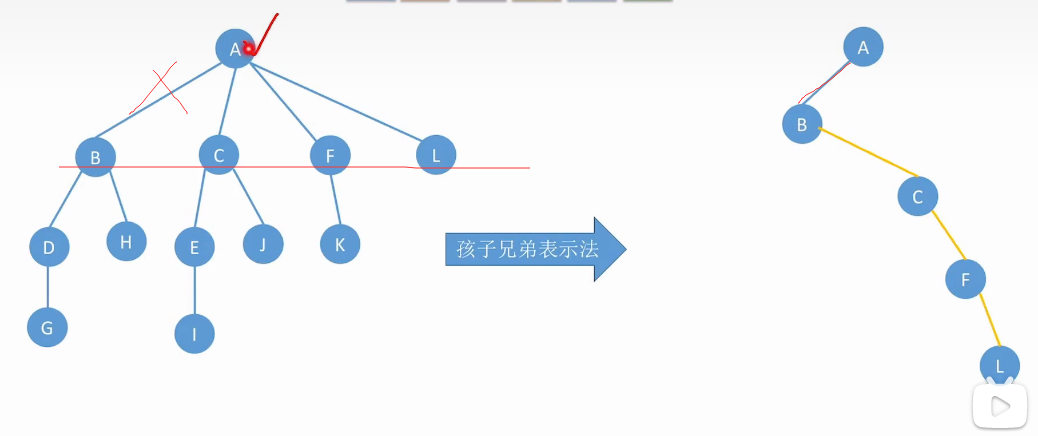
二叉树-孩子兄弟表示法来表示

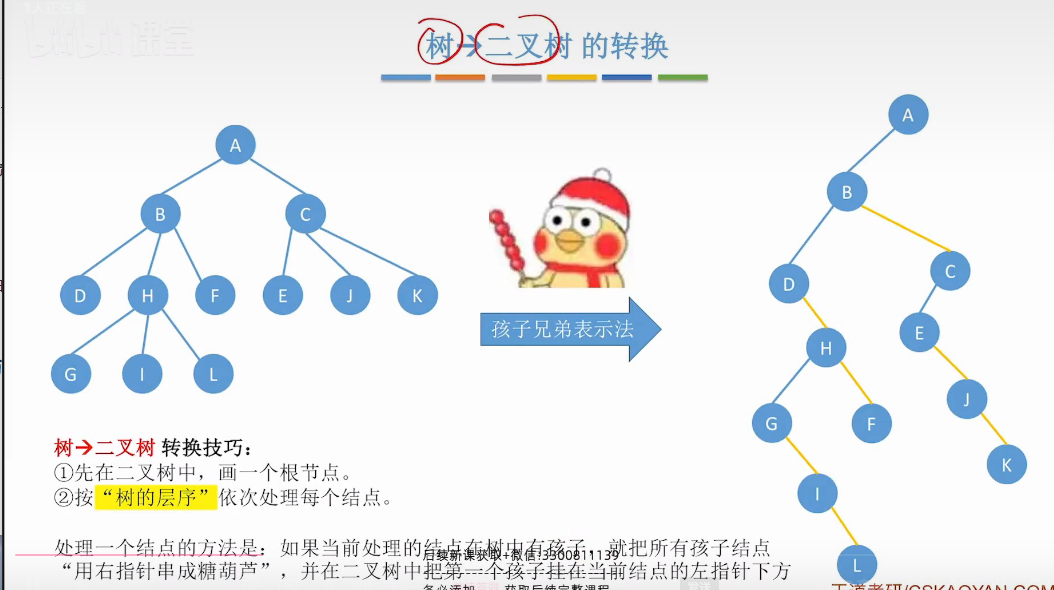
串糖葫芦就是右指针串

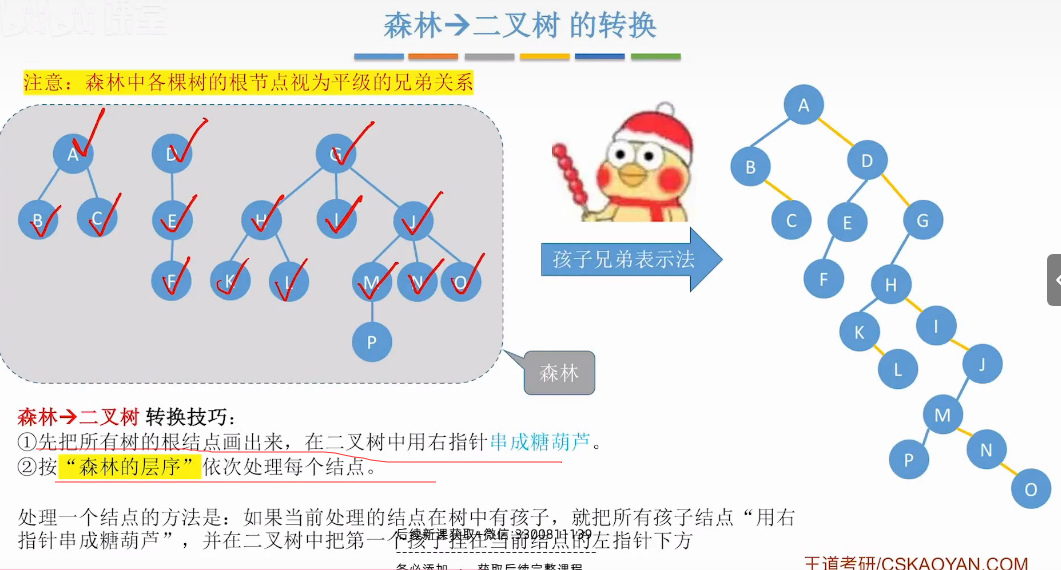
森林转二叉树

ps:基本不变-就是根节点线串完后-依次遍历每个节点下的数据

二叉树转树

1.过程转换

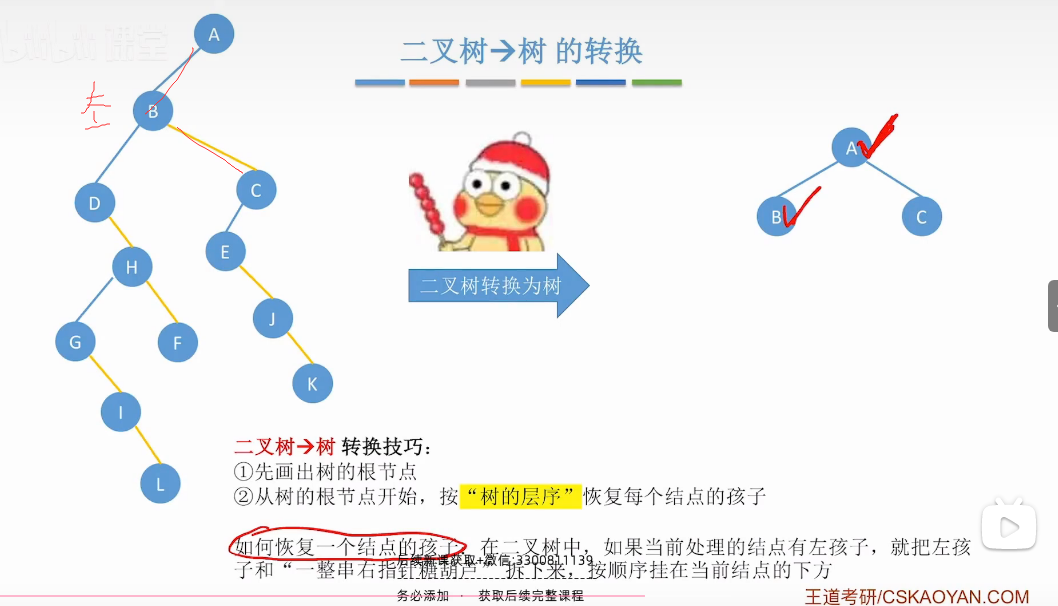
A->B右节点有节点-把整个右节点拆下来-同级

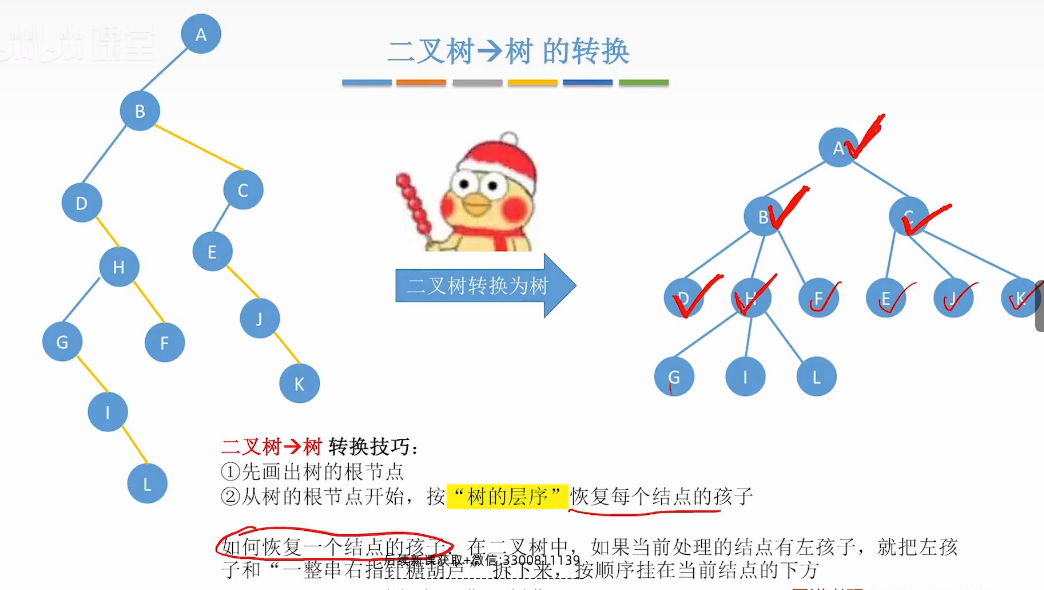
层次顺序恢复

二叉树转森林

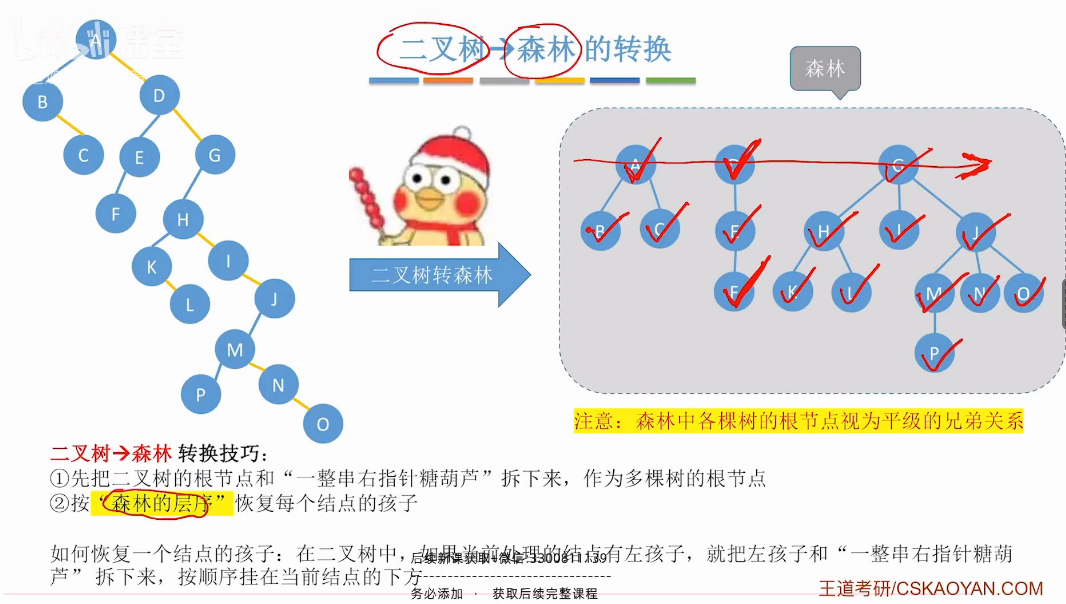
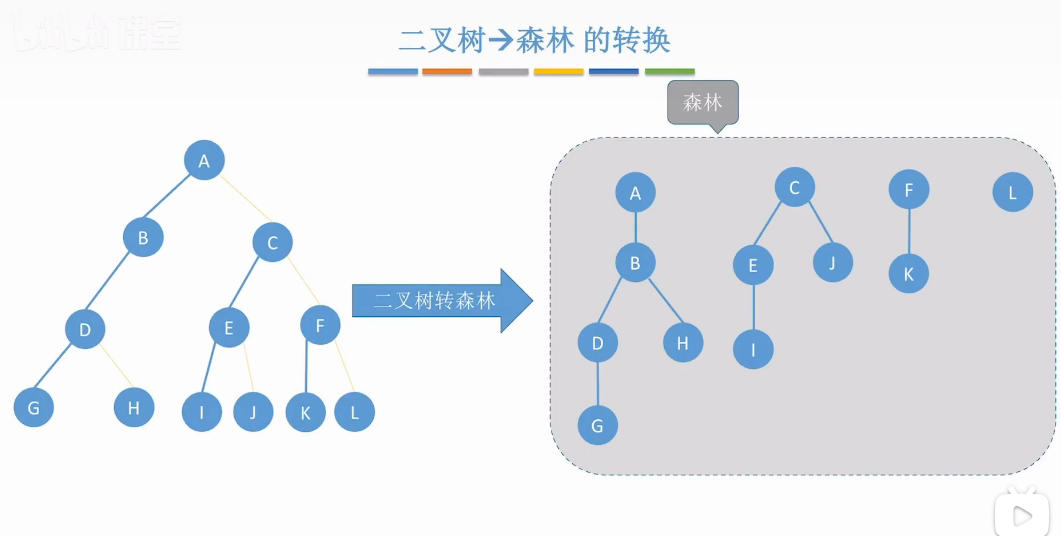
小结

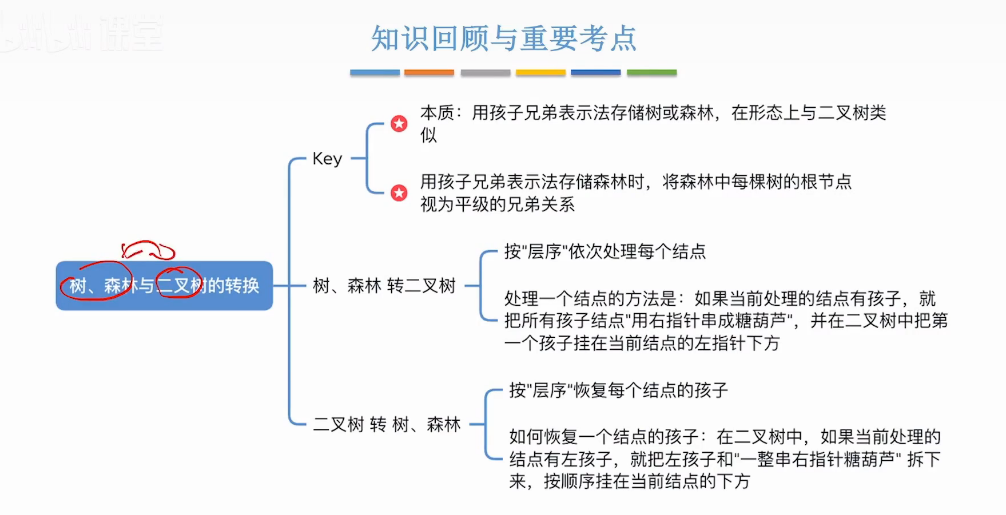
注意-简化二叉树下-什么是树-什么是森林

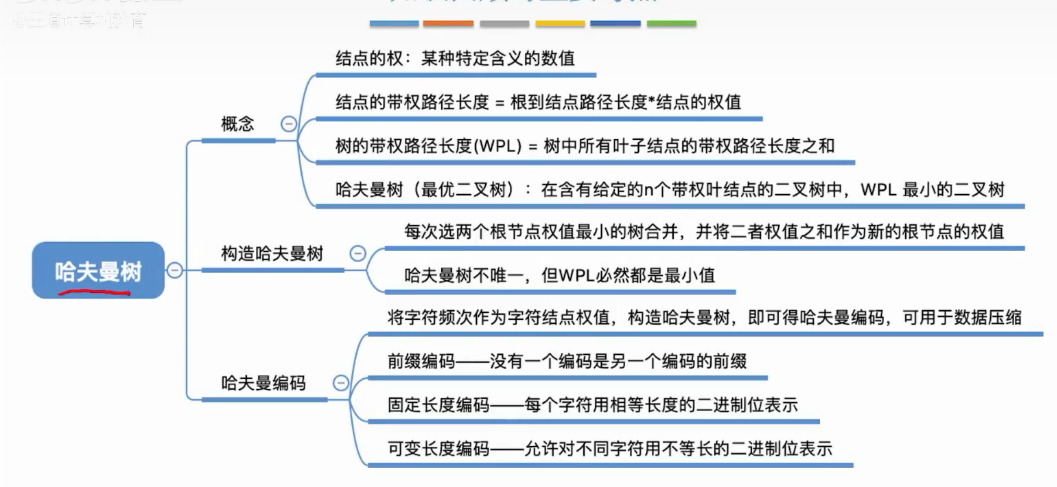
6.7 哈夫曼树

带权路径长度

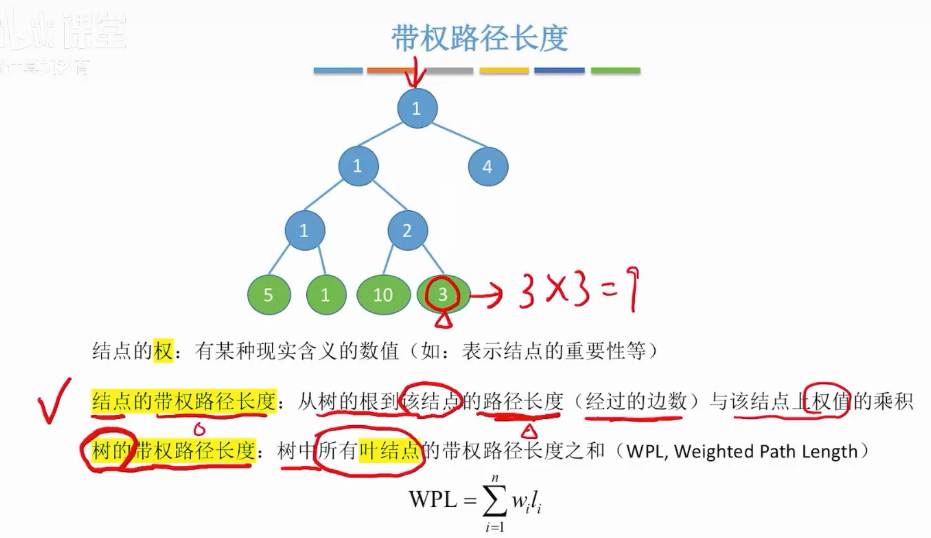
树的带权路径长度

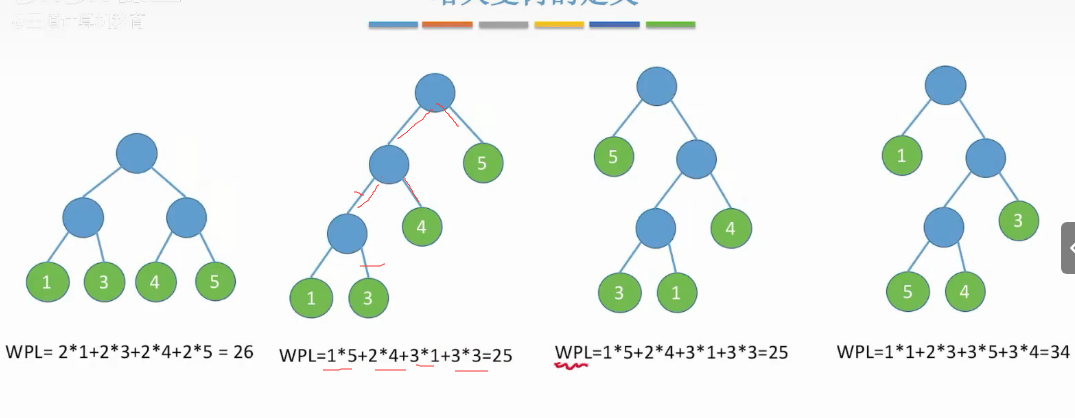
*叶子节点的权值-根节点到达叶子经过的边数-之和

哈夫曼树的定义-构造

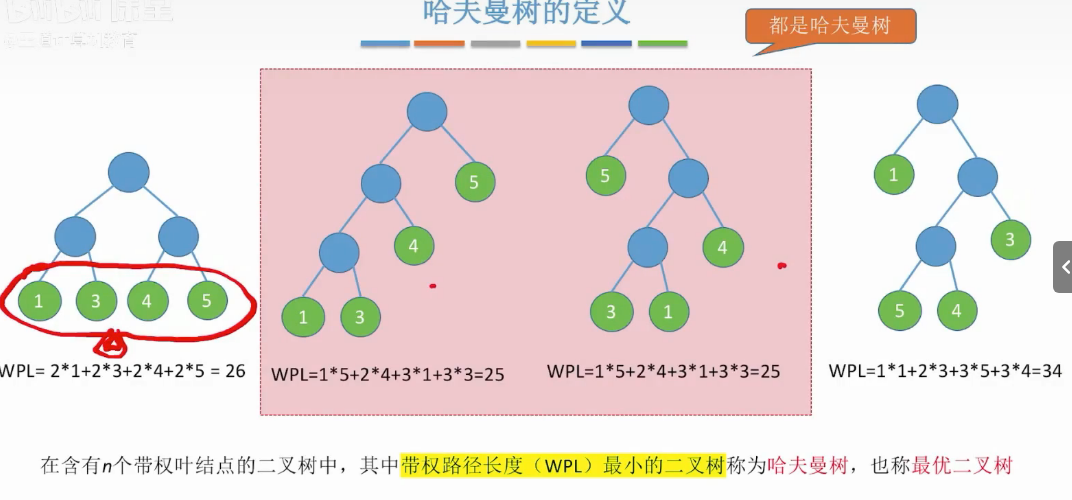
哈夫曼树的构造

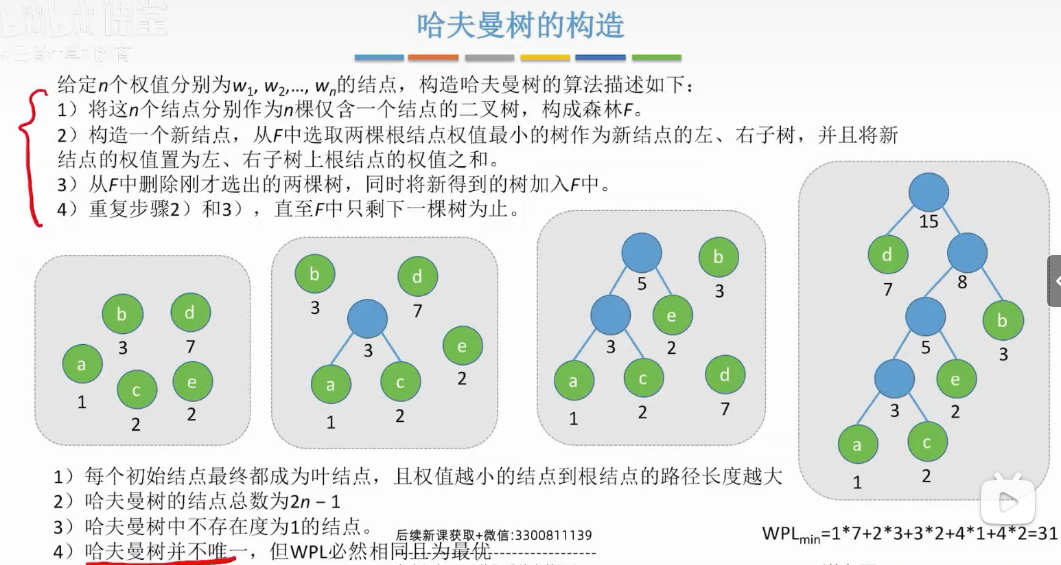
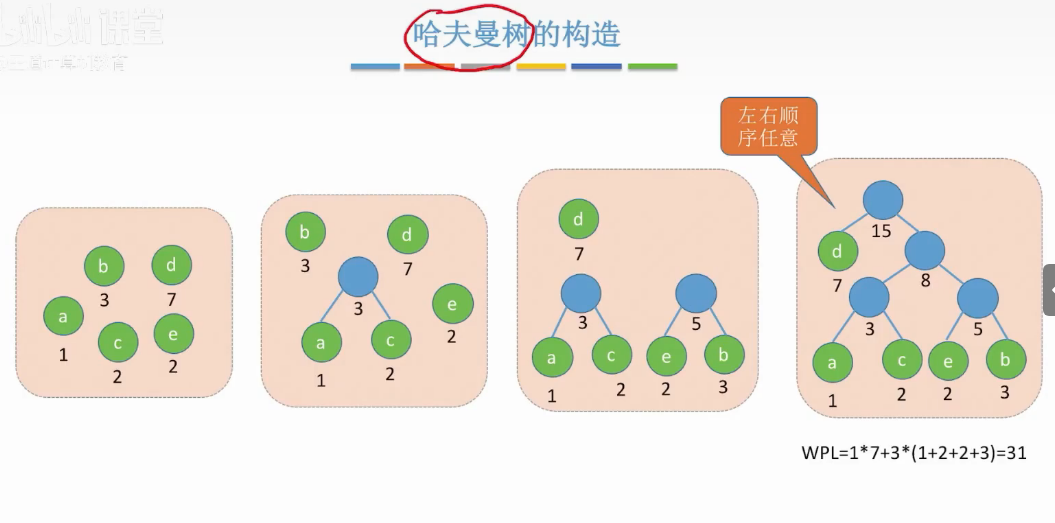
将最小和的叶子节点结合-会生成新的节点-其中-必须是叶子节点

哈夫曼树的编码

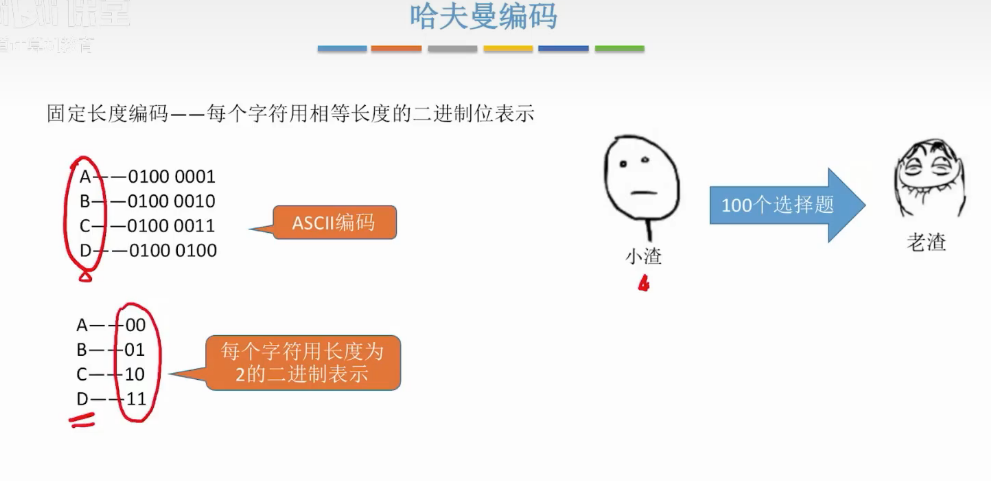
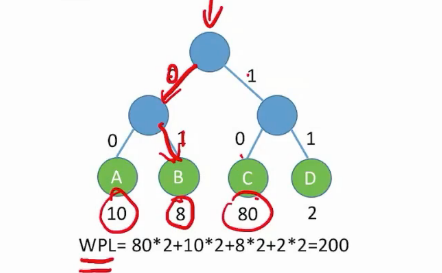
2.重新规范ABCD编码

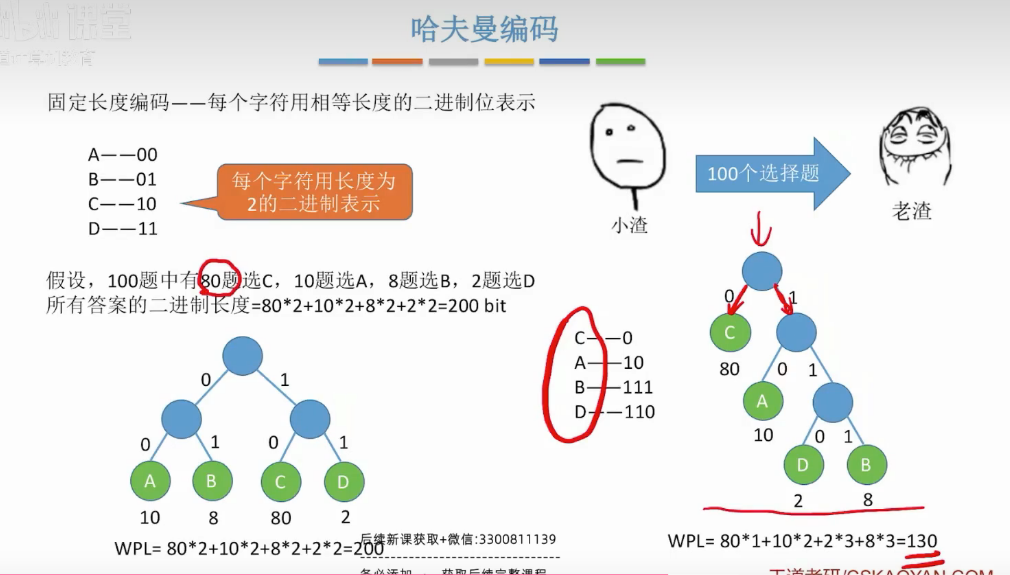
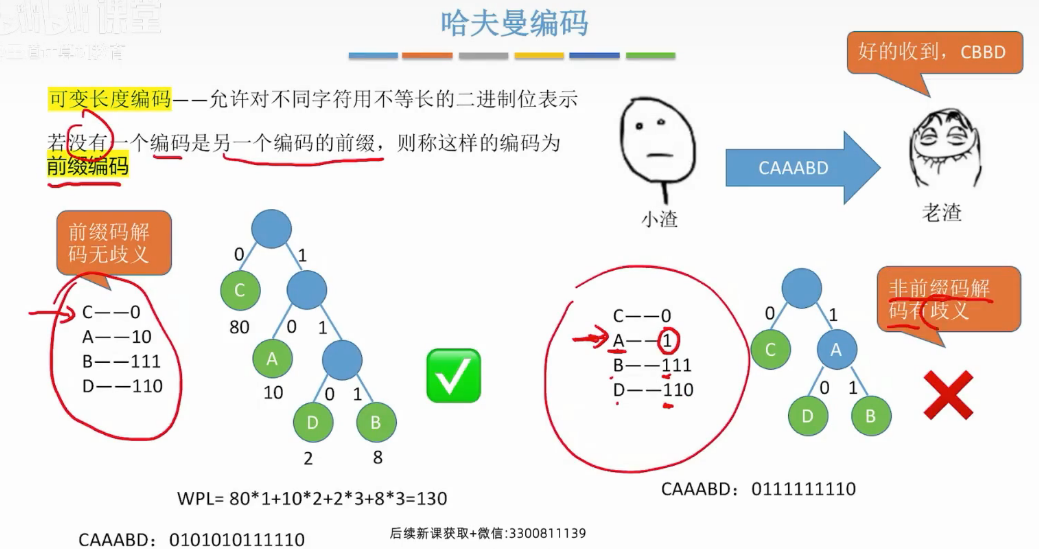
前缀编码

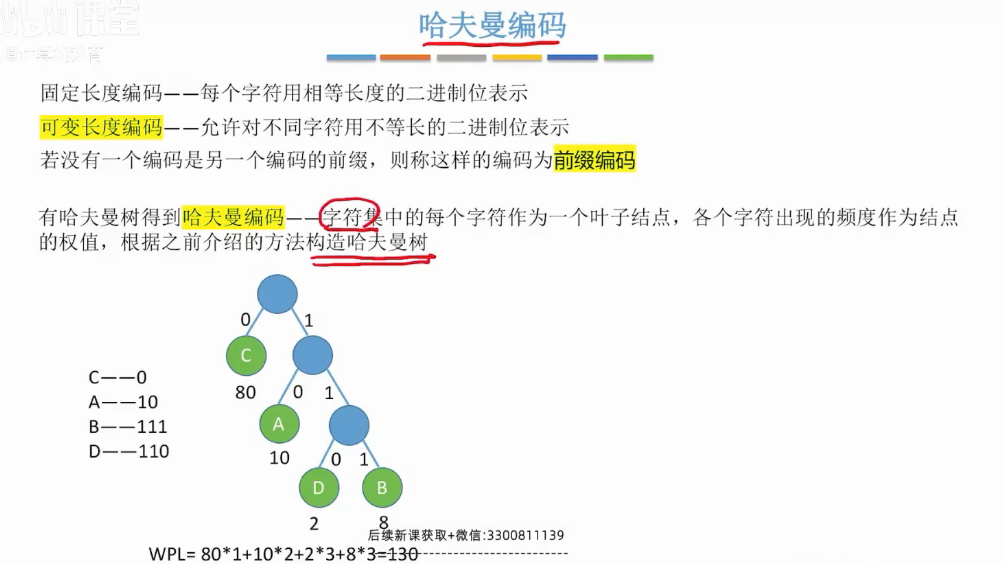
总结