线性表 下
双线性表链表和循环双链表
2.4.1双链表
算法不同的只有插入和删除
1
2
3
4
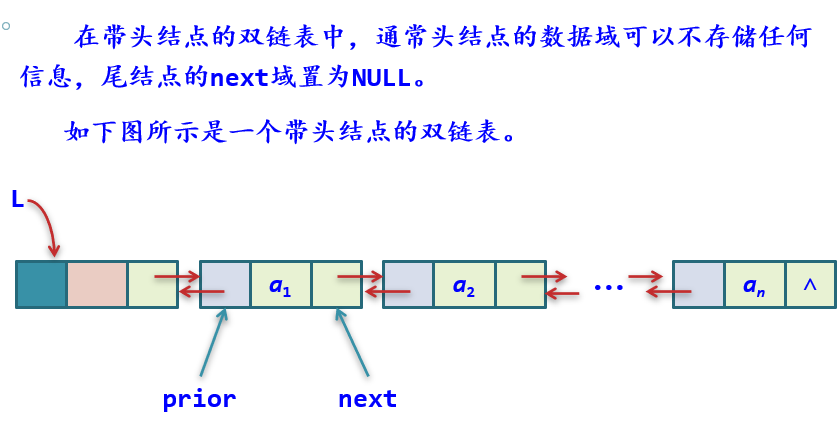
| 双链表中用两个指针表示结点间的逻辑关系。
指向其前驱结点的指针域prior。
指向其后继结点的指针域next。
|
1
2
3
4
5
6
| T9 ypedef struct node
{ ElemType data;
struct node *prior,*next;
} DLinkNode;
|
双链表基本运算算法
1.初始化线性表运算算法
1
| 创建一个空的双链表,它只有一个头结点,由L指向它,该结点的next域和prior域均为空,data域未设定任何值。
|
1
2
3
4
5
6
| void InitList(DLinkNode *&L)
{ L=(DLinkNode *)malloc(sizeof(DLinkNode));
L->prior=L->next=NULL;
}
|
2.销毁线性表运算算法
1
| 销毁一个双链表中的所有结点的算法思路与单链表的销毁算法相同。
|
1
2
3
4
5
6
7
8
9
| void DestroyList(DLinkNode *&L)
{ DLinkNode *pre=L,*p=pre->next;
while (p!=NULL)
{ free(pre);
pre=p; p=p->next;
}
free(pre);
}
|
3.求线性表长度运算算法
1
2
3
4
5
6
7
8
9
10
| int GetLength(DLinkNode *L)
{ int i=0;
DLinkNode *p=L->next;
while (p!=NULL)
{ i++;
p=p->next;
}
return i;
}
|
4.求线性表中第i个元素运算算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| int GetElem(DLinkNode *L,int i,ElemType &e)
{ int j=0;
DLinkNode *p=L;
if (i<=0) return 0;
while (p!=NULL && j<i)
{ j++;
p=p->next;
}
if (p==NULL) return 0;
else
{ e=p->data;
return 1;
}
}
|
5.按值查找运算算法
1
2
3
4
5
6
7
8
9
10
11
| int Locate(DLinkNode *L,ElemType e)
{ DLinkNode *p=L->next;
int i=1;
while (p!=NULL && p->data!=e)
{ p=p->next;
i++;
}
if (p==NULL) return 0;
else return i;
}
|
6.插入元素运算算法
1
| 先在双链表中查找到第i-1个结点,若成功找到该结点(由p所指向),创建一个以x为值的新结点s,将s结点插入到p之后即可。
|
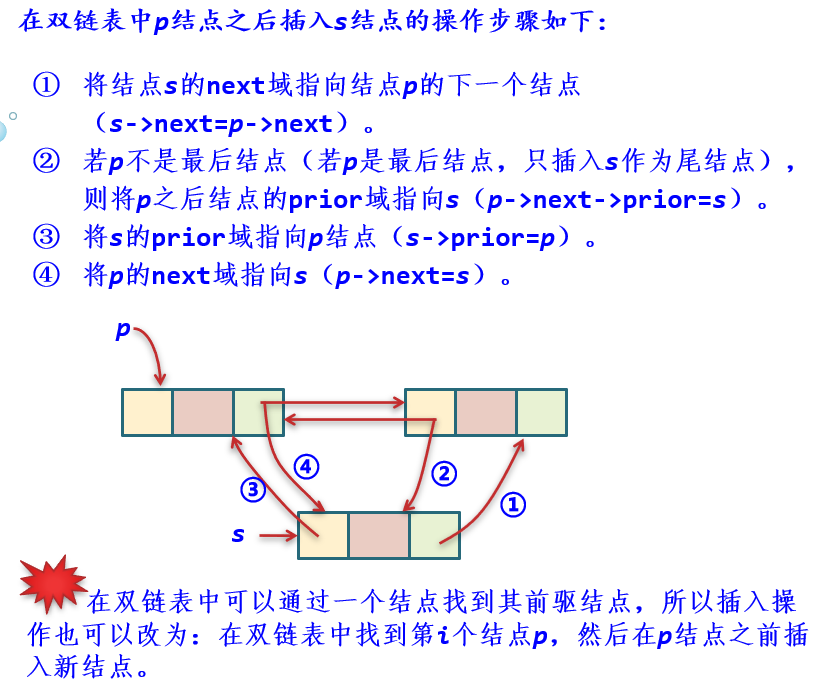
若插入节点为i位置 需要修改i内存的前 后指针
同时i-1位置的next i+1的前置 prior
需要修改四个位置-找到2个内存地址
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| int InsElem(DLinkNode *&L,ElemType x,int i)
{ int j=0;
DLinkNode *p=L,*s;
if (i<=0) return 0;
while (p!=NULL && j<i-1)
{ j++;
p=p->next;
}
if (p==NULL) return 0;
else
{
s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=x;
s->next=p->next;
if (p->next!=NULL)
p->next->prior=s;
s->prior=p;
p->next=s;
return 1;
}
}
|
6.删除结点运算算法
1
| 先在双链表中查找到第i个结点,若成功找到该结点(由p所指向),通过前驱结点和后继结点的指针域改变来删除p结点
|
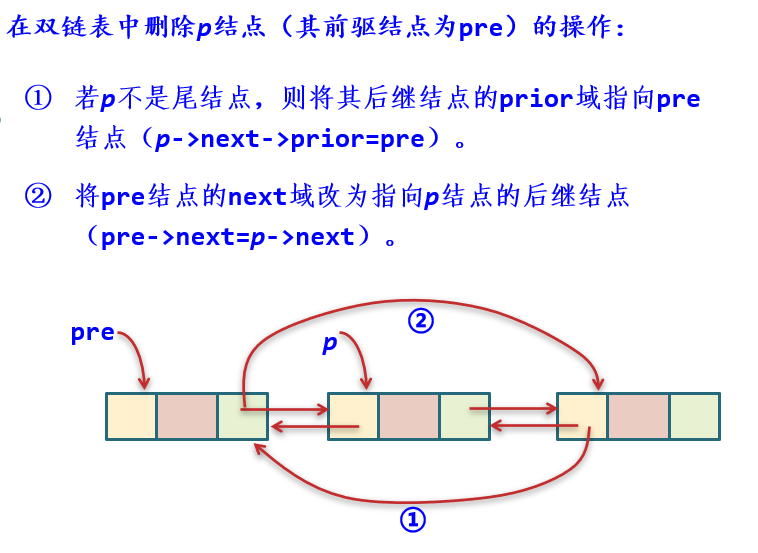
假设删除i -i-1的next指向改变 i+1的prior改变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| int DelElem(DLinkNode *&L,int i)
{ int j=0;
DLinkNode *p=L,*pre;
if (i<=0) return 0;
while (p!=NULL && j<i)
{ j++;
p=p->next;
}
if (p==NULL) return 0;
else
{ pre=p->prior;
if (p->next!=NULL)
p->next->prior=pre;
pre->next=p->next;
free(p);
return 1;
}
}
|
7.输出线性表运算算法
1
2
3
4
5
6
7
8
9
| void DispList(DLinkNode *L)
{ DLinkNode *p=L->next;
while (p!=NULL)
{ printf("%d ",p->data);
p=p->next;
}
printf("\n");
}
|
整体创建双链表的算法
1.头插法
1
2
3
4
| 从一个空双链表(含有一个L指向的头结点)开始。
读取数组a(含有n个元素)中的一个元素,生成一个新结点s,将读取的数据元素存放到新结点的数据域中。
然后将新结点s插入到当前链表的表头上。
再读取数组a的下一个元素,采用相同的操作建立新结点s并插入到双链表L中,直到数组a中所有元素读完为止
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void CreateListF(DLinkNode *&L,ElemType a[],int n)
{ DLinkNode *s;int i;
L=(DLinkNode *)malloc(sizeof(DLinkNode));
L->next=NULL;
for (i=0;i<n;i++)
{ s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=a[i];
s->next=L->next;
s->prior=L;
if (L->next!=NULL)
L->next->prior=s;
L->next=s;
}
}
|
2.尾插法
1
2
3
4
5
| 从一个空双链表(含有一个L指向的头结点)开始。
读取数组a(含有n个元素)中的一个元素,生成一个新结点s,将读取的数据元素存放到新结点的数据域中。
然后将新结点s插入到当前链表的表尾上。
再读取数组a的下一个元素,采用相同的操作建立新结点s并插入到双链表L中,直到数组a中所有元素读完为止。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void CreateListR(DLinkNode *&L,ElemType a[],int n)
{ DLinkNode *s,*tc; int i;
L=(DLinkNode *)malloc(sizeof(DLinkNode));
tc=L;
for (i=0;i<n;i++)
{ s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=a[i];
tc->next=s;
s->prior=tc;
tc=s;
}
tc->next=NULL;
}
|
双链表的算法设计示例
2.22
2.18
2.4.4循环双链表
了解循环双链表
1
2
3
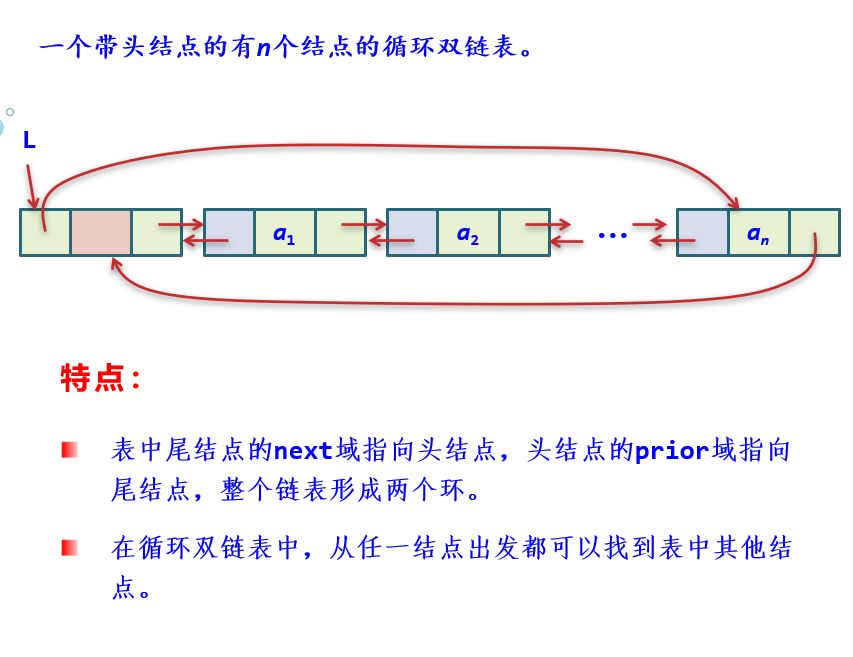
| 与循环单链表一样,也可以使用循环双链表。
循环双链表的结点类型与双链表的结点类型相同,也采用前面声明的DLinkNode类型。
|
1.初始化线性表运算算法
1
| 创建一个空的循环双链表,它只有一个头结点,由L指向它,该结点的next域和prior域均指向该头结点,data域未设定任何值
|
1
2
3
4
5
| void InitList(DLinkNode *&L)
{ L=(DLinkNode *)malloc(sizeof(DLinkNode));
L->prior=L->next=L;
}
|
2.销毁线性表
1
2
3
4
5
6
7
8
9
| void DestroyList(DLinkNode *&L)
{ DLinkNode *pre=L,*p=pre->next;
while (p!=L)
{ free(pre);
pre=p; p=p->next;
}
free(pre);
}
|
3.求线性表长度运算算法
1
2
3
4
5
6
7
8
9
10
| int GetLength(DLinkNode *L)
{ int i=0;
DLinkNode *p=L->next;
while (p!=L)
{ i++;
p=p->next;
}
return i;
}
|
4.**求线性表中第i个元素运算算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int GetElem(DLinkNode *L,int i,ElemType &e)
{ int j=1;
DLinkNode *p=L->next;
if (i<=0) return 0;
while (p!=L && j<i)
{ j++;
p=p->next;
}
if (p==L) return 0;
else
{ e=p->data;
return 1;
}
}
|
5.按值查找运算算法
1
2
3
4
5
6
7
8
9
10
11
12
| int Locate(DLinkNode *L,ElemType x)
{ int i=1;
DLinkNode *p=L->next;
while (p!=L && p->data!=x)
{ p=p->next;
i++;
}
if (p==L) return 0;
else return i;
}
|
6.插入元素运算算法
1
2
3
4
| 先在循环双链表L中查找第i个结点p及其前驱结点pre,用j记录p结点的序号。
当p==L且i>j+1时表示i参数错误(如循环双链表中只有3个结点,当i>4时出现这种错误)。
当成功找到pre结点后,创建data域为x的结点s。
在pre结点之后插入s结点
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| int InsElem(DLinkNode *&L,ElemType x,int i)
{ int j=0;
DLinkNode *pre=L,*p=pre->next,*s;
if (i<=0) return 0;
while (p!=L && j<i-1)
{ j++;
pre=p; p=p->next;
}
if (p==L && i>j+1) return 0;
else
{ s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=x;
pre->next->prior=s;
s->next=pre->next;
pre->next=s;
s->prior=pre;
return 1;
}
}
|
7.删除元素运算算法
1
| 先在循环双链表L中查找第i个结点p,若成功找到后通过其前驱结点pre将p结点删除。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| int DelElem(DLinkNode *&L,int i)
{ int j=1;
DLinkNode *p=L->next,*pre;
if (i<=0) return 0;
if (L->next==L) return 0;
while (p!=L && j<i)
{ j++;
p=p->next;
}
if (p==L) return 0;
else
{ pre=p->prior;
p->next->prior=pre;
pre->next=p->next;
free(p);
return 1;
}
}
|
8.输出线性表运算算法
1
2
3
4
5
6
7
8
9
| void DispList(DLinkNode *L)
{ DLinkNode *p=L->next;
while (p!=L)
{ printf("%d ",p->data);
p=p->next;
}
printf("\n");
}
|
循环双链表的算法设计示例
2.24
2.25
线性表的应用
1.步骤
1
2
3
4
5
| 当通过分析确定了求解问题中数据逻辑结构为线性关系时,设计线性表应用程序的一般步骤如下:
(1)根据求解功能的特点设计相应的存储结构。
(2)设计相应的基本运算算法。
(3)设计求解问题的主程序。
|
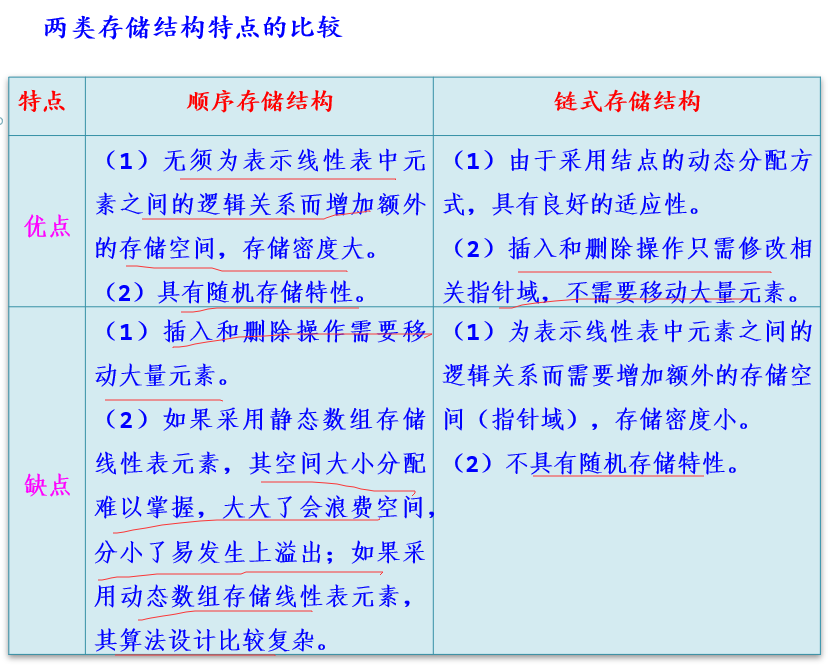
2.顺序存储和线性存储区别
java线性结构探究
顺序存储结构的代表:
- 数组(Array) 在 Java 中,数组是一种基础的顺序存储结构,元素连续存储在内存中。
- ArrayList
ArrayList 是 Java 中基于数组实现的动态数组,容量可以根据需要自动扩展。
- String java 中的
String 本质上是一个字符数组,它也是顺序存储的经典例子。
- Vector
Vector 和 ArrayList 类似,但它是线程安全的。它内部也是基于数组实现的。
- Stack Java 中的
Stack 是基于 Vector 实现的,元素按顺序存储,具有先进后出的特点。
链式存储结构的代表:
- LinkedList
LinkedList 是 Java 中的双向链表,节点通过指针相互链接。
- HashMap 中的链表
HashMap 和 HashTable 的底层实现之一是链表,在发生哈希冲突时,将多个冲突的键值对存储在链表中。
- Queue Java 中的
LinkedList 也可以用作队列,队列是先进先出(FIFO)的数据结构。
- PriorityQueue
PriorityQueue 是一种特殊的队列,元素按优先级排序,而不是按插入顺序存储。




