数据结构概论 01

数据结构概论

第一章-概述

1.1概述

1.1.1:什么是数据结构

数据与信息

  • 数据是信息的载体，可以被计算机识别、存储和加工处理。数据包括文字、表格、图像等形式。
  • 信息是数据的内涵，即数据所表达的意义。例如，成绩单中某次考试的成绩是数据，但平均分就是信息。

数据元素和数据项

  • 数据元素是数据的基本单位（有时称为元素、结点或记录等），通常作为一个整体进行处理。例如，一个学生的成绩单包含了若干个数据元素。
  • 数据对象是具有相同类型的数据元素的集合。
  • 数据项是数据元素的不可分割的最小标识单元。例如，一个学生记录可以包含姓名、学号等数据项。

数据的结构

  • 数据的结构化表示方式便于数据的存储和处理。在数据结构中，除非特别指明，数据通常都是数据对象。

：

数据结构的定义和内容

数据结构是相互之间存在一种或多种特定关系的数据元素的集合。在计算机中，数据元素不是孤立存在的，而是相互之间通过某种关系连接，形成一个整体结构。数据结构的主要内容包括以下三个方面：

  1. 逻辑结构：描述数据元素之间的逻辑关系，是数据结构的抽象形式。逻辑结构通常通过图形表示，例如线性结构、树形结构和图结构等。
  2. 存储结构：也称为“物理结构”或“存储映像”，是将数据的逻辑结构映射到计算机存储器中的形式。数据的存储结构决定了数据在计算机内存中的布局方式，包括顺序存储、链式存储等。
  3. 数据运算：指的是在数据结构上进行的各种操作，是数据结构的功能体现。例如，常见的数据操作包括查找、插入、删除、排序等。这些操作通常是通过特定的算法在存储结构上实现的。
1.1.2 逻辑结构探究

逻辑结构的定义

  • 逻辑结构是指数据元素之间的逻辑关系，它表示数据元素之间如何相互关联。逻辑结构不涉及数据在计算机中的存储方式，只描述数据元素之间的关系。

  • 逻辑结构的四种类型

    1. 集合结构：所有数据元素之间没有任何关系。

    2. 线性结构：所有数据元素之间存在一对一的关系。

    3. 树形结构：数据元素之间存在一对多的层次关系。

    4. 图形结构（网状结构）：数据元素之间存在多对多的任意关系。

      逻辑结构的表示方法-书中是公式

      • 线性结构（Linear Structures）：

        • 定义：在这种结构中，数据元素之间具有一对一的关系，即每个数据元素除了第一个和最后一个之外，都有唯一的前驱和后继。常见的线性结构有数组、链表、栈和队列等。
        • 特点：数据按照一定的顺序排成一条直线，每个元素只有一个前驱和一个后继（除第一个和最后一个元素）。
        • 例子：数组是一种典型的线性结构，数据元素按顺序存储在内存中，元素之间的关系通过索引来表示。

        树形结构（Tree Structures）：

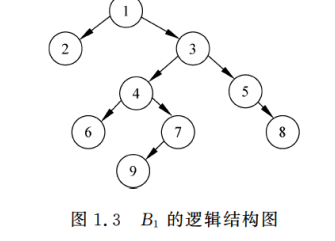
        • 定义：在这种结构中，数据元素之间具有一对多的层次关系。树形结构中，每个元素称为“节点”，顶层节点称为“根节点”，其余节点有且仅有一个父节点，可能有多个子节点。
        • 特点：数据以层级形式组织，每个节点有一个父节点和零个或多个子节点，除了根节点外，每个节点只有一个父节点。
        • 例子：二叉树是一种常见的树形结构，其中每个节点最多有两个子节点（左子节点和右子节点）。

        图形结构（Graph Structures）：

        • 定义：在这种结构中，数据元素之间可以有任意多的关系，数据元素称为“节点”或“顶点”，它们之间的关系称为“边”。
        • 特点：数据元素之间的关系不再是简单的一对一或一对多，可以是多对多的关系。图可以是有向的或无向的，有环的或无环的。
        • 例子：社交网络中的好友关系可以用图来表示，用户是节点，好友关系是边。

        逻辑表示：学生按学号从小到大排列，每个学生只有一个前驱和一个后继（除了第一个和最后一个）。这种逻辑表示方式告诉我们数据元素的相对关系和结构。

        物理表示：在计算机中，可以用一个数组来顺序存储这些学生信息，或者用一个链表来链式存储这些学生信息。

      • 逻辑结构图的表示

      • ：

        • 数据逻辑结构可以通过二元组 (D,R)(D,R) 来表示，其中 DD 是数据元素的集合，RR 是数据元素之间的逻辑关系集合。

      • cf1f08b63104c88f692a527f21308624

53667aed05cf29e331afb013cad99845

1.1.3 存储结构探究

存储结构定义
  1. 存储结构定义：
    • 数据的存储结构是指数据逻辑结构在计算机存储器中的表示，它也被称为物理结构。

  1. 存储结构与逻辑结构的关系：

    • 同一种逻辑结构可以设计成多种不同的存储结构。
    • 在不同的存储结构中，实现相同运算的算法可能会有所不同。

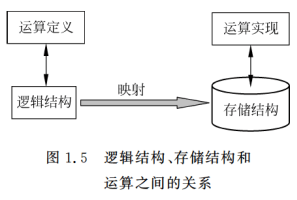
  2. 逻辑结构、存储结构和运算之间的关系：

    • 逻辑结构通过映射到存储结构，进而实现具体的运算。
    • 运算定义和运算实现之间存在映射关系，逻辑结构是运算定义的基础，而存储结构是运算实现的基础。

37a0f47f6721fdf22db0eb82ac7865b2

顺序表

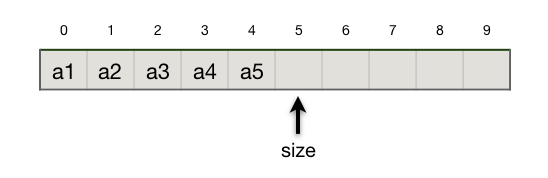
../../_images/311_sequence_list.png

顺序存储结构通过连续存储单元实现数据的逻辑结构映射，具有存储空间节省和快速随机存取的优点，但同时也存在修改不便的缺点。这种存储方式适用于数据元素数量固定或变动较少的场景。

  1. 顺序存储结构定义：
    • 顺序存储结构是使用一组连续的存储单元来存放所有数据元素，其中逻辑上相邻的元素在物理存储上也是相邻的。
    • 元素之间的逻辑关系通过存储单元地址的相邻关系隐含表示，即将数据的逻辑结构直接映射到存储结构。
  2. 顺序存储结构的实现示例：
    • 以“Score”逻辑结构为例，假设每个元素占用30字节（B），从100号存储单元开始，按低地址到高地址方向存储。
  3. 顺序存储结构的优点：
    • 节省存储空间：分配给数据的存储单元全部用于存放元素值，元素之间的逻辑关系表示不占用额外存储空间。
    • 随机存取：可以实现对数据元素的快速随机存取。给定元素的逻辑序号，可以在常量时间内查找到对应的元素值。
  4. 随机存取的计算公式：
    • 存储地址计算公式为： LOC(ai)=p+(i−1)×kL**OC(a**i)=p+(i−1)×k
    • 其中，kk 是每个元素所占的存储单元数，pp 是第一个元素所占存储单元的首地址。
  5. 顺序存储结构的缺点：
    • 不便于修改：在进行元素的插入或删除操作时，可能需要移动一系列元素，这在大规模数据操作时效率较低。

ArrayList- Vector CopyOnWriteArrayList

如上都实现了 List 接口，并具有顺序访问的特点。

链式存储

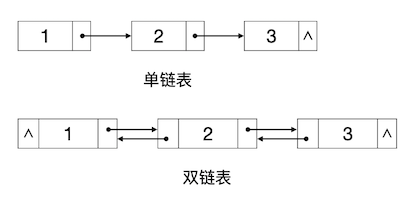
../../_images/317_linkedlist.png

  1. 链式存储结构定义：

    • 链式存储结构不要求所有元素在内存中连续存放，每个节点独立存储，不需要占用一整块连续的存储空间。
    • 为了表示节点之间的关系，每个节点包含一个或多个指针字段，用于存放相邻节点的存储地址。
  1. 链式存储结构的优点：
    • 便于修改：在进行插入、删除操作时，只需修改节点的指针域，不需要移动节点本身。
  2. 链式存储结构的缺点：
    • 存储空间利用率较低：分配给数据元素的存储单元中有一部分被用来存放节点之间的逻辑关系。
    • 不能进行随机存取：由于逻辑上相邻的节点在存储器中不一定相邻，因此不能对节点进行随机存取。

LinkedList 双向链表

ConcurrentLinkedQueue 线程安全的非阻塞队列

LinkedBlockingQueue 和 LinkedBlockingDeque

索引结构

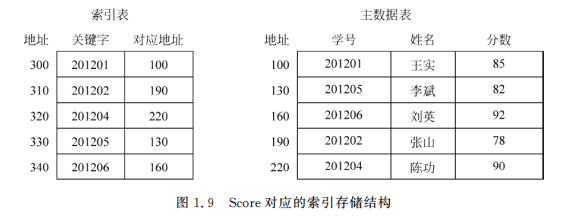
  1. 索引存储结构定义：

    • 索引存储结构是在存储数据（主数据表）的同时，建立一个附加的索引表。
    • 索引表中的每一项称为索引项，通常包含关键字和对应的地址。

  2. 索引项的一般形式：

    • 索引项的一般形式为：(关键字, 对应地址)
    • 索引表中的关键字有序排列（如递增），每个关键字的对应地址指向该关键字记录在数据表中的存储地址。

  3. 索引存储结构的查找过程：

    • 在进行关键字（如学号）查找时，先在索引表中快速查找（因为索引表中按关键字有序排列，可以采用二分查找）到相应的关键字。
    • 然后通过对应地址在数据表中找到该记录的数据。

  4. 索引存储结构的优点：

    • 查找效率高：由于索引表中关键字有序排列，可以采用二分查找等高效查找算法。

  5. 索引存储结构的缺点：

    • 增加时间和空间开销：需要建立索引表，从而增加了存储空间的开销。
    • 维护成本：在数据表更新（插入、删除、修改）时，需要同步更新索引表，增加了维护成本。
    • 2efbc94f98d8f0fe441857b7f84d636d

img

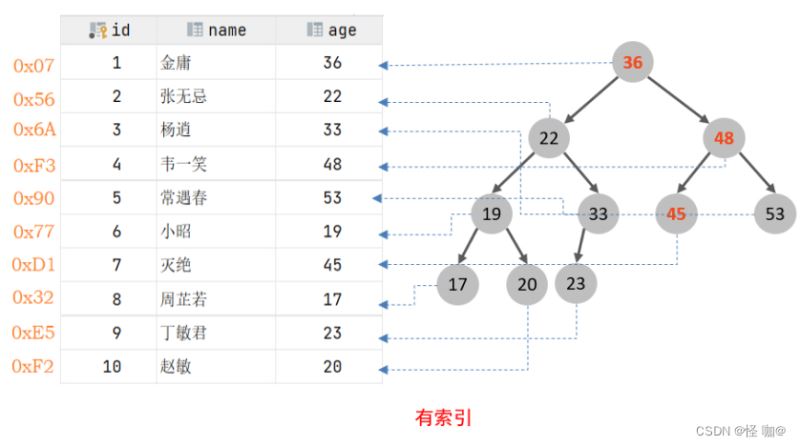
HashMap / TreeMap 键可以视作索引，值为实际数据类似

哈希结构

  1. 哈希存储结构定义：

    • 哈希存储结构根据元素的关键字来确定其存储地址。
    • 通过哈希函数 H(key)H(k**ey)（或散列函数）计算关键字对应的函数值，该函数值用作元素的存储地址。

  2. 哈希函数的选择：

    • 以学号作为自变量，选择一个合适的哈希函数，例如 h(学号)=学号−201201h(学号)=学号−201201。

  3. 哈希存储结构的查找过程：

    • 要查找学号为 idi**d 的学生记录，只需计算 h(id)h(i**d)，以它为地址在哈希表中直接找到该学号的学生记录。

  4. 哈希存储结构的优点：

    • 查找速度快：只要给出待查找节点的关键字，就可以立即计算出对应记录的存储地址。
    • 存储效率高：只存储数据元素本身，不存储数据元素之间的逻辑关系。

  5. 哈希存储结构的缺点：

    • 冲突处理：不同的关键字可能通过哈希函数计算得到相同的地址，需要处理这种“冲突”。
    • 哈希函数的选择：选择合适的哈希函数和冲突解决策略是关键。

  6. 哈希存储结构的应用场合：

    • 适用于要求对数据能够进行快速查找、插入的场合。

HashMap 和 HashSet 提供了基础的哈希功能；LinkedHashMap 和 LinkedHashSet 在保证哈希效率的同时维护插入顺序；ConcurrentHashMap 提供线程安全的哈希表实现，而 WeakHashMap 和 IdentityHashMap 提供了特定应用场景的支持。

1.14 数据运算

  1. 数据运算的定义：
    • 数据运算是施加于数据的操作，它包括对数据进行的各种处理活动。
  2. 运算的两个部分： 分离思想
    • 运算定义：描述运算的功能和目的，是抽象的描述，不涉及具体的实现细节。
    • 运算实现：在特定的数据存储结构上设计算法来实现这些运算，是具体的实现步骤。

1.15 数据结构 数据类型 和抽象数据类型

1.数据结构

数据结构 :带结构的数据元素的集合 包含数据逻辑 存储逻辑 运算运算逻辑

2.数据类型

数据类型显示或隐式的定义了数据的存储格式 数据范围 允许进行的计算

1.c++基本数据类型

省

2.指针类型

int * a=&b; -> b(地址)->123(真实数据)

int ** =&a; 嵌套类-不知道行不行

3.c++数组类型

int a[10];

4.结构体类型

struct t{

int a;

char a;

}

集体占的大小还要适配内存对齐-防止缓存失效解决

5.共用体类型

省

6.自定义类型

typedef struct ttudent{
}studtype

别名 ->根结构体差不多

3.抽象数据类型

抽象数据类型是一种数据模型的抽象，描述了数据类型的操作和功能，而不关心其具体实现。ADT提供了一组操作和数学模型，用于定义数据类型的行为和性质。ADT定义时包含了操作的逻辑及功能描述，具体实现则留给程序设计者。

dcc57cf60c33af3dd920d15376ccad4a

ps:说白了就是想像一个结构体出来-但是没有具体实现

1.1 总结

概念上的东西，没刷题不知道-但是非常概念的就是-抽象数据类型 数据运算 概述和数据结构

1.2 算法和算法分析

1.2.1算法及描述

1.算法特性

算法-对特定问题求解步骤的描述

算法设计满足目标

正确性：算法必须能够正确执行其规定的功能和性能要求，这是最重要的标准。

可使用性：算法应易于理解和使用，即具有用户友好性。

可读性：算法应该便于人的理解，逻辑必须明确、简单、结构良好。

健壮性：算法应具备很好的容错能力，即使遇到异常数据，也能处理或防止崩溃。

高效性与低存储性：算法应在执行时间和存储空间上高效，对同一问题，算法的效率越高越好，同时要求其存储消耗低。

算法特性

4a5032bae80dd2445ae8a06cb1ea232e

2.算法描述

算法描述:算法可由多种语言来描述-

7121e96e74080a4416b2c76d17c7908a

如上-代码-s=s+i->修改是地址的值-栈压得值-可修改call栈外的局部变量-

ps:前提是s=s+1-是对外部指针指向的数据操作-而不是拷贝了一份-(cpp好久没看过了)

这里应该表面 -算法的输入 输出 是s-同一个吗-不知道，文字太多不想看

1.2.3算法分析

1.算法时间复杂度

时间复杂度（Time Complexity）是用来估计一个算法运行时间的一个指标，表示算法执行所需时间相对于输入规模的增长关系。它反映了算法随着输入数据量增大，运行时间增加的情况。

时间复杂度通常使用大O符号（Big O Notation）表示，如 O(1)、O(n)、O(n^2) 等。大O符号描述了最坏情况下算法的运行时间。

常见时间复杂度及其含义

  1. O(1) - 常数时间复杂度

    • 算法的执行时间不依赖于输入数据的规模。例如，访问数组中的某个元素。

    • 示例：a = array[5] 这个操作总是执行一个步骤，因此时间复杂度是 O(1)。

    • 2.O(n) - 线性时间复杂度

    • 算法的执行时间随着输入数据的规模 n 线性增长。也就是说，输入数据翻倍，运行时间也会翻倍。

    • 示例：一个简单的 for 循环遍历 n 个元素。

    1
    2
    python复制代码for i in range(n):
        print(i)

O(n^2) - 二次时间复杂度

  • 算法的执行时间与输入规模的平方成正比。通常出现在嵌套循环中，外层和内层都循环 n 次。
  • 示例：双重嵌套循环遍历二维数组。
1
2
3
4
python复制代码
for i in range(n):
    for j in range(n):
        print(i, j)

O(log n) - 对数时间复杂度

  • 算法的执行时间随着输入数据的规模呈对数增长，通常出现在“二分”算法中，比如二分查找。每次操作将问题规模减半。
  • 示例：在一个排序数组中查找元素的位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import java.util.Arrays;

public class LogarithmicTimeExample {
    public static void main(String[] args) {
        int[] array = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
        int target = 7;
        int result = binarySearch(array, target);
        
        if (result == -1) {
            System.out.println("Element not found.");
        } else {
            System.out.println("Element found at index: " + result);
        }
    }

    // 二分查找实现
    public static int binarySearch(int[] array, int target) {
        int left = 0;
        int right = array.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (array[mid] == target) {
                return mid;
            }

            if (array[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return -1; // 未找到目标元素
    }
}

O(n log n) - 线性对数时间复杂度

  • 常见于高效的排序算法，如快速排序（Quick Sort）和归并排序（Merge Sort）。它的时间复杂度是 n 和 log n 的乘积。

  • 示例：归并排序。

  • import java.util.Arrays;

public class MergeSortExample {
    public static void main(String[] args) {
        int[] array = {38, 27, 43, 3, 9, 82, 10};
        mergeSort(array, 0, array.length - 1);
        System.out.println("Sorted array: " + Arrays.toString(array));
    }

    // 归并排序算法
    public static void mergeSort(int[] array, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2;

            mergeSort(array, left, mid); // 递归排序左半部分
            mergeSort(array, mid + 1, right); // 递归排序右半部分

            merge(array, left, mid, right); // 合并两部分
        }
    }

    // 合并两个子数组的函数
    public static void merge(int[] array, int left, int mid, int right) {
        int n1 = mid - left + 1;
        int n2 = right - mid;

        int[] leftArray = new int[n1];
        int[] rightArray = new int[n2];

        for (int i


    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14

    **O(2^n) - 指数时间复杂度**

    - 随着输入规模增加，算法运行时间以指数方式增长。通常出现在解决递归问题（如斐波那契数列）时。

    - 示例：递归计算斐波那契数列。

    - ```
      def fibonacci(n):
          if n <= 1:
              return n
          else:
              return fibonacci(n-1) + fibonacci(n-2)
      
    

  **O(n!) - 阶乘时间复杂度**

  最糟糕的时间复杂度，通常出现在解决组合问题时，如全排列生成或旅行商问题（TSP）。

  示例：生成一个数组的所有排列。

如何计算时间复杂度

  1. 分析算法的基本操作：找出算法中最常执行的基本操作（如循环中的一次迭代）。
  2. 确定基本操作的执行次数：计算该操作在最坏情况下的执行次数。
  3. 去掉低阶项和常数：只关注增长速度最快的项，并忽略常数因子（如 5n 和 n 都视为 O(n)）。

总结

O(1) - 常数时间复杂度

O(log n) - 对数时间复杂度

O(n) - 线性时间复杂度

O(n log n) - 线性对数时间复杂度

O(n^2) - 二次时间复杂度

O(n^3) - 三次时间复杂度

O(2^n) - 指数时间复杂度

O(n!) - 阶乘时间复杂度

案例:https://www.cnblogs.com/Agtw/p/17173051.html -

2.算法空间复杂度

1.空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用
了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计
算规则基本跟实践复杂度类似，也使用大O渐进表示法.-
就是一段函数在堆栈中开辟的堆栈大小

空间复杂度衡量了算法所需的额外内存空间，帮助我们理解和优化程序的内存使用。

选择合适的算法时，既要考虑时间复杂度，也要考虑空间复杂度，特别是在处理大规模数据或资源有限的情况下。

O(1) - 常数空间复杂度

1
2
3
4
5
6
7
8
9
10
public int findMax(int[] array) {
    int max = array[0]; // O(1) 空间复杂度，仅使用一个额外变量
    for (int i = 1; i < array.length; i++) {
        if (array[i] > max) {
            max = array[i];
        }
    }
    return max;
}

O(log n) - 对数空间复杂度

O(n) - 线性空间复杂度\

1
2
3
4
5
6
7
public int[] copyArray(int[] array) {
    int[] newArray = new int[array.length]; // O(n) 空间复杂度，因需分配与输入规模相同的空间
    for (int i = 0; i < array.length; i++) {
        newArray[i] = array[i];
    }
    return newArray;
}

O(n log n) - 线性对数空间复杂度

O(n^2) - 二次空间复杂度

O(n^3) - 三次空间复杂度

O(2^n) - 指数空间复杂度

O(n!) - 阶乘空间复杂度

1.3 数据程序结构设计

1.3.1 数据结构程序设计步骤

  1. 设计数据结构程序的步骤：
    • 第一步：分析问题的数据和求解功能，使用抽象数据类型（ADT）来描述问题，包括数据逻辑结构和运算定义。
    • 第二步：设计逻辑结构对应的存储结构。
    • 第三步：在选定的存储结构上设计实现运算定义的算法。

1.3.2 应用程序结构

![a1b9aa105652fe4d7386574ca6429d89](G:\360MoveData\Users\nixg\Documents\Tencent Files\1332425260\nt_qq\nt_data\Pic\2024-09\Ori\a1b9aa105652fe4d7386574ca6429d89.png)

总结

这些文件提供了关于数据结构、算法以及它们在程序设计中应用的全面概述。以下是核心内容的整理：

  1. 数据结构的定义：

    • 数据结构是存在特定关系的数据元素集合，包括数据项和数据元素。

  2. 数据结构的组成：

    • 包括数据逻辑结构、数据存储结构和数据运算。 +1

  3. 数据逻辑结构的分类：

    • 集合、线性结构、树状结构和图形结构，其中树状和图形结构是非线性结构。

  4. 数据存储结构的类型：

    • 顺序存储、链式存储、索引存储和哈希存储。 +1 *

  5. 存储结构的设计：

    • 存储结构设计需考虑存储元素及其逻辑关系，同一逻辑结构可对应多个存储结构。

  6. 抽象数据类型：

    • 由数据逻辑结构和抽象运算组成。

  7. 算法的定义：

    • 算法是特定问题求解步骤的描述，具有有限性、确定性、可行性、输入性和输出性。

  8. 算法描述：

    • 算法通常用C/C++函数的形式描述，复杂算法可能需要多个函数。

  9. 算法设计考虑：

    • 明确算法的输入和输出，通常作为函数的形参和返回值。

  10. 算法条件的有效性：

    • 条件有效时返回1（真），否则返回0（假）。

  11. 算法分析：

    • 包括时间复杂度和空间复杂度分析，目的是提高算法效率。

  12. 时间复杂度分析：

    • 选取基本运算，求其频度，取最高阶并置系数为1。

  13. 存储结构与算法的关系：

    • 良好的存储结构可以提高算法效率。

  14. 求解问题的步骤：

    • 建立抽象数据类型，设计合理的存储结构，在此基础上设计高效算法。

本文大部分内容来自数据结构 数据结构简明教程(第2版)

由本人经过gdp润色后+加上自己理解所抄录笔记-

第一章算是润色把 自我感觉有用的就是1

.数据结构的定义和组成

逻辑结构+存储结构

算法-算法的五要素 算法时间复杂度和空间复杂度

这些内容以前学比特数据结构1h学完

数据结构
数据结构概论 01
http://example.com/2024/09/12/数据结构/
作者
John Doe
发布于
2024年9月12日
许可协议